top trees まとめ

top trees のまとめブログです。

本文中でいくつかの用語に勝手に日本語の文字列を当てます。

2023-11-22 新たに文献[18]に言及しました。

元祖 top trees

fully-dynamic な森に関して、 Alstrup 等^{[18] (*1)} によって top tree が定義されました。この章ではその定義と重要な事実を確認します。

辺を $1$ 個以上含む根なし無向木 (underlying tree) を $T$ 、 $T$ の頂点を $0$ 個以上 $2$ 個以下選んで 外端点 (external boundary verticies) とし、その集合を $\partial T$ とします。このとき、以下で述べる条件を満たす二分木 $R$ を構築できるので、それを top tree と呼びます。

$T$ の部分木^(*2) $C$ について、 $C$ に含まれる頂点 $v$ が 端点 (boundary vertex) であるとは、次のいずれかを満たすことです。

• $v$ は外端点である。^(*3)
• $T$ に含まれて $C$ に含まれない頂点が $v$ に隣接している。

部分木 $C$ が cluster であるとは、 $C$ の端点が $2$ 個以下であることです。 cluster の様子が全体の木 $T$ と外端点の集合 $\partial T$ に依存するため $C_{(T, \partial T)}$ と表されるべきですが、ここでは省略します。^(*4)します。

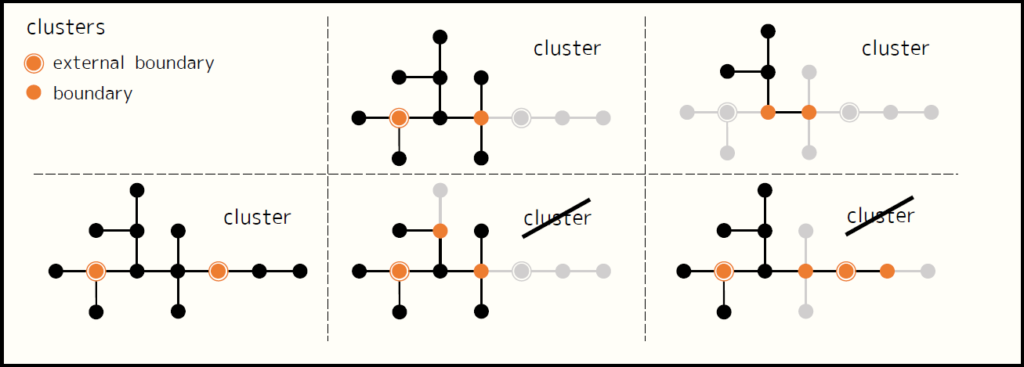
top tree $R$ が満たすべき条件は次です。

• $R$ の各頂点は $T$ の cluster である。
• $R$ の葉は、 $T$ の辺を $1$ つだけ含む。
• $R$ の葉でない頂点について、その $2$ つの子の共通部分は、ちょうど $1$ つの頂点である。
• $R$ の葉でない頂点は、その $2$ つの子の合併である。
• $R$ の根は、 $T$ そのものである。

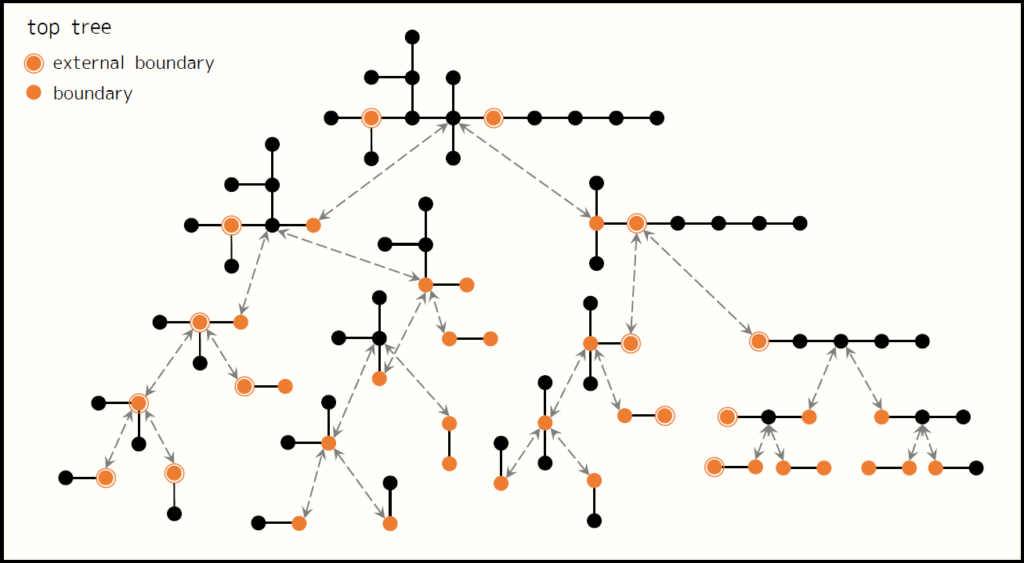
さらに、ユーザーが次の操作を定義するとします。

• join( $A$ , $B$ ) ： $A$ , $B$ はそれぞれ top tree の根である。これらを子にもつ新たな top tree の根を作成し、それを返す。
• split( $C$ ) ： $C$ は top tree の根であり、葉でない。根 $C$ を削除し、その $2$ つの子を返す。
• create ： underlying tree の $1$ つの辺からなる cluster から新たな top tree を作り、それを返す。
• destroy ： 辺 $e$ を含む top tree を削除する。

以上を踏まえて、 top trees は次のインターフェースを提供します。

• link( $(v,w)$ ) ： underlying tree に辺 $(v,w)$ を追加。
• cut( $e$ ) ： underlying tree の辺 $e$ を削除。
• expose( $v$ , $w$ ) ： 外端点を $2$ 頂点 $v$ , $w$ に変更する。

これに関して、文献[1] で述べられたおそらく最も重要な事実である Theorem 1 の内容は次です。

操作対象の木のサイズを $n$ とする。 top tree の高さを $O(\log n)$ に保つ。このとき link,cut,expose それぞれは、 $O(1)$ 回の create, destroy と $O( \log n )$ 回の join, split からなる操作列で実現でき、その操作を $O( \log n )$ 時間で決定できる。 top trees が占める空間は $n$ に対して線形である。 link,cut,expose からなる $k$ 個を一連の操作として実行するとき、これらの上界は $k$ 倍される。(Alstrup 等^[1])

文献[1] の Theorem 1 以降では、 top trees のさらなる機能が紹介されています。

top tree 上で二分探索 select( $f$ ) が可能です。 $f$ はユーザーが与える関数で、木全体の辺集合を $2$ つの cluster に分割したものを与えると目的の辺が含まれる方を選びます。すると top tree は $f$ を用いて目的の辺を求めます。計算量は目的の辺からなる cluster の深さに対して線形時間です。外端点が $1$ 個以下のときは underlying tree の全域を、 $2$ 個のときはその間の単純パス内を探索できます。下図は select 実行中に深さ $1$ だけ進む動作の例です。

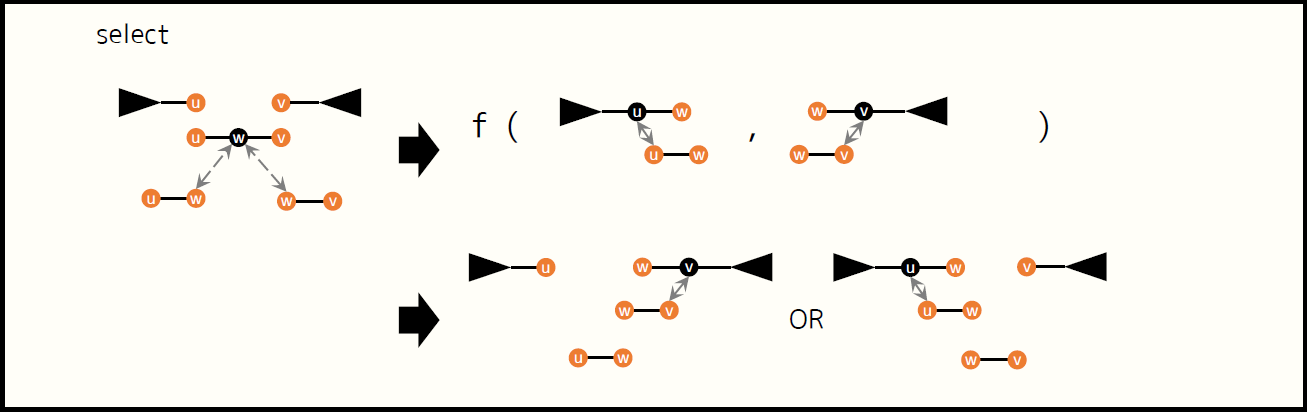
文献[1] ではさらに、頂点に label を付ける方法や Theorem 1 より一般的な計算量解析、および具体的な top trees の構成方法が示されていますが、私は内容を確認していません。

---

(*1) Jacob Holm. Kristian de Lichtenberg. Top-trees and dynamic graph algorithms. https://di.ku.dk/forskning/Publikationer/tekniske_rapporter/tekniske-rapporter-1998/98-17.pdf(2023-11-22 閲覧) の Chapter 3 （の 3.1 よりも前の部分）には first presented in と書いてあるし、たぶん [18] が最初なんじゃないかな…

(*2) (無向木の)部分木：連結な誘導部分グラフ

(*3) top tree の前身である topology tree では、この外端点の概念が無かった。 see also [18]

(*4) 2023-11-24 修正。 [1] にこの表記があると思い込んでここを書いたが、改めて見るとそのような数式は書かれていなかった。

top trees のいろんな実装

• (1) Alstrup 等^[1] による実装
  • クエリ当たり $O( \log n)$ 時間で、償却は不要。
  • top tree の高さ $O( \log n)$ を保証。
  • [未検証]：私はこれをよく調べていないし、競技プログラミングの文脈での利用例を見たことがない。
• (2) Tarjan と Werneck^[2] による self-adjusting top trees
  • 償却 $O( \log n)$ 時間。
  • 頂点に隣接する辺の順番 (circular order) も管理できる。
  • 機能性のわりに実装が複雑だが、実行時の効率は競プロで実用的。
• (3) Tarjan と Werneck^[2] による simplified self-adjusting top trees
  • circular order が不要な場合に大幅単純化。
  • 償却 $O( \log n)$ 時間。競プロで実用的。
  • niuez^[4] が解説した。
• (4) Sleater と Tarjan^[3] による link/cut tree の実装において dashed edges を splay tree^[3] で管理するバリエーション ^[6][7][8]
  • Alstrup 等による top trees の定義に対応しないものもある^[6] が、 underlying tree の頂点や辺に結び付けた情報のみに注目する限り top trees と同様のインターフェースで管理できると考えられる。
  • (3) と同様の計算量解析ができるため償却 $O( \log n)$ 時間と考えられている一方、[6][7]では証明できたとは述べられていない。競プロで実用的。
  • splaying で平衡する link/cut tree をベースにする。 underlying tree の辺の情報を管理する場合は対応するノードを足せばよい。
  • いくつかの構築方法が考えられ、 simplified self-adjusting top trees もその $1$ つである。
  • self-adjusting top trees に比べて、葉木由来の実装の難しさが除かれる場合がある。

実用上 top trees が最適でない場合

• (1) 静的木で、データも静的な場合、全方位木 dp ^[9] がより適している可能性。
  • 基本的に $O(n)$ 時間。
  • インターフェースによる制約が top trees よりも緩い。
• (2) 静的木を扱うとき、 HL 分解を利用するほうが高速である可能性。
  • 例えば静的な木に対して点更新・パス最小値のクエリを処理する場合、平易な HL 分解による解法は毎クエリ $O( (\log n)^2)$ 時間しか保証できないが、それでも link/cut tree や top tree を用いるよりもはるかに高速。
• (3) 比較的単純なクエリを扱うとき、 link/cut tree のほうが高速である可能性。^{[11][13][14][16][17]}
  • パス外を含めた集約やパス外からの遅延伝播を dashed edge 到達時に処理。^[10]
  • ただし search の代替には dashed edges を二分探索木で管理する必要がある。^[12]

特に (3) は現状、 top trees の機能をほぼ完全に代替しつつ top trees より高速な実装^[12]があります。従って (3) の代わりに top trees を利用する利点は小さいです。

逆に、 expose,link,cut,search のうちで (3) で代替できない機能があるとすれば、 search のうち、 dashed edges を標準ライブラリの平衡二分探索木で管理すると不都合がある場合のみです。この問題点を素直に対策すると top trees のいろんな実装 の (4) が得られます。

問題例

現状 (2022/1/25)、以下の問題はすべて top trees を実装したものより実行時間が短い提出があり、 実用上 top trees が最適でない場合 にあてはまります。

• [13] Library Checker Dynamic Tree Vertex Add Path Sum https://judge.yosupo.jp/problem/dynamic_tree_vertex_add_path_sum
  • 動的木
  • 頂点重み
  • パス重み和

• [14] Library Checker Dynamic Tree Subtree Add Subtree Sum https://judge.yosupo.jp/problem/dynamic_tree_subtree_add_subtree_sum
  • 動的木
  • 頂点重み
  • $1$ つの辺を切って得られる部分木に一様加算
  • $1$ つの辺を切って得られる部分木の重み和

• [15] yukicoder No.1787 Do Use Dynamic Tree https://yukicoder.me/problems/no/1787
  • 静的木
  • 頂点重み

• [16] yukicoder No.902 Query ζone https://yukicoder.me/problems/no/902
  • 動的木
  • 辺重み

• [17] yukicoder No.772 Dynamic Distance Sum https://yukicoder.me/problems/no/772
  • 動的森
  • 頂点重み
  • 重心

実装例

• beet-aizu による。 (C++) https://beet-aizu.github.io/library/toptree/toptree.cpp
• niuez^[4] による。 (Rust) https://github.com/niuez/toptree-rust

参考文献/引用

[1] ALSTRUP, Stephen, et al. Maintaining information in fully dynamic trees with top trees. Acm Transactions on Algorithms (talg), 2005, 1.2: 243-264. : https://arxiv.org/abs/cs/0310065

[2] TARJAN, Robert Endre; WERNECK, Renato Fonseca F. Self-adjusting top trees. In: SODA. 2005. p. 813-822. : http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.87.9754&rep=rep1&type=pdf

[3] Sleator, D. D., & Tarjan, R. E. (1985). Self-adjusting binary search trees. Journal of the ACM (JACM), 32(3), 652-686.：https://www.cs.cmu.edu/~sleator/papers/self-adjusting.pdf

[4]

続編 https://niuez.hatenablog.com/entry/2019/08/05/114511

[5]

[6]

[7] yosupot. yukicoder No.772 Dynamic Distance Sum 解説. ：https://paper.dropbox.com/doc/Top-Tree-ZWtQdaUh68tou1iu0YdRG 2022/1/25閲覧.

[8] noshi91. a tweet. 2022. ：https://twitter.com/noshi91/status/1483744348886171651 2022/1/27閲覧.

[9] keymoon. 【全方位木DP】明日使える便利な木構造のアルゴリズム. 2020. ：https://qiita.com/keymoon/items/2a52f1b0fb7ef67fb89e 2022/1/26閲覧.

[10] QCFium. Link-cut treeで部分木更新をする. 2020.：https://qiita.com/QCFium/items/83d6d3a85df485451e78 2022/1/26閲覧.

[11] QCFium. [Tutorial] Subtree lazy propagation on the link-cut tree. 2020.： https://codeforces.com/blog/entry/80145 2022/1/27閲覧.

[12] ei1333. QTREE LCT + Dynamic Distance Sum. 2019. ：https://ei1333.hateblo.jp/entry/2019/07/09/005011 2022/1/27閲覧.

[13] Library Checker. Dynamic Tree Vertex Add Path Sum. ：https://judge.yosupo.jp/problem/dynamic_tree_vertex_add_path_sum

[14] Library Checker. Dynamic Tree Subtree Add Subtree Sum. ：https://judge.yosupo.jp/problem/dynamic_tree_subtree_add_subtree_sum

[15] yukicoder. No.1787 Do Use Dynamic Tree.： https://yukicoder.me/problems/no/1787

[16] yukicoder. No.902 Query ζone.： https://yukicoder.me/problems/no/902

[17] yukicoder. No.772 Dynamic Distance Sum. ： https://yukicoder.me/problems/no/772

[18] ALSTRUP, Stephen, et al. Minimizing diameters of dynamic trees. In: Automata, Languages and Programming: 24th International Colloquium, ICALP’97 Bologna, Italy, July 7–11, 1997 Proceedings 24. Springer Berlin Heidelberg, 1997. p. 270-280. https://link.springer.com/chapter/10.1007/3-540-63165-8_184

---

不具合の連絡は twitter:@NachiaVivias へ