AGC はユーザー解説書けない (2022/06/03)
2022/08/23追記 rating 3200 以上のユーザは書けるらしいです (!?)
2023/08/02追記 rating 2800 以上のユーザは書けるようになったので、 05/16 に投稿しました
AtCoder Grand Contest 002 D – Stamp Rally

典型テクニック
- disjoint set union (DSU) のマージ過程を表す木
- ダブリングによる lowest common ancestor (LCA) の計算
- 答えで二分探索
他の解法
並列二分探索 $O(M (\log N)\alpha (N) + Q \log N )$
2022/09/14更新 $\alpha(N)$ を掛けるところを間違えていました。
公式解説は DSU の時系列上の並列二分探索を用いています。計算量は $O(M (\log N)\alpha (N) + Q \log N )$ などとすべきだと思いますが、 $O((Q+M) \log (N))$ と書かれています。英語解説には(丁寧にも)アッカーマン関数の逆関数の因数は無視してもよいと書かれているので、これに従って日本語解説でも無視したものと思われます。
面白い
公式解説の影響か(あるいは流行りの加減か)、同様の解法とソースコードかつ、 DSU による因数 $\alpha(N)$ を無視した計算量を記す解説が多く見つかりました。
部分永続 union-find $O((M+Q) (\log N)^2)$
けんちょん (drken) さんは部分永続 union-find で問題を解いています。部分永続なので、オンラインで二分探索ができます。
weighted union heuristic によって union-find の木の高さが $O(\log N)$ であり、よって issame の計算量は $O(\log N)$ です。 size は高々サイズ $N$ のリスト上の二分探索ですから計算量は $O(\log N)$ です。これを用いて時間で二分探索することで全体で計算量 $O((M+Q) (\log N)^2)$ を達成しています。
平方分割 $O((M+Q) \sqrt{M} \alpha(N))$
hiko3r さんの解説は平方分割による解法で、クエリをオンラインで処理します。 $B=\Theta(\sqrt{M})$ として、 $B$ 辺ごとに union-find の状態を保存します。各クエリに対しては、まず $B$ 辺ずつ進む場合を二分探索し、中間の高々 $B$ 辺は愚直に追加(し、後で revert )します。
解答例が空になっていますが、ページのソースコードの該当部分からリンクを発見できました。
https://github.com/Hoikoro/procon/blob/master/AGC002D.cpp
この解法は union-find を $\Theta(\sqrt{M})$ 個保存するためメモリをかなりたくさん使いますが、 kmjp さんが解説する平方分割はクエリをオフラインで処理する代わりに union-find を $1$ 個しか使いません。
詳細は省略します。計算量は $O((M+Q) \sqrt{M} \alpha (N))$ です。
マージ過程を表す木を用いた解法
計算量 $O(N \log N + M \alpha (N) + Q (\log N)^2)$
DSU のマージ過程を表す森を構築します。 union-find を用いて計算量 $O(N+M\alpha (N))$ で構築できます。元のグラフが連結なので、この森は木です。
重み $w$ 以下の辺しか通らないと仮定したとき、頂点 $p$ からスタートして移動できる領域を表すノードは、マージ過程を表す木において頂点 $p$ 自身またはその祖先です。このノードを求めるためには、各頂点 $p$ と各非負整数 $d$ について $p$ の $2^d$ 段階親を求めておき、二分探索すればよいです。テーブルの構築は計算量 $O(N \log N)$ です。
これで $w$ を決めると兄弟が移動できる領域の頂点数を計算量 $O( \log N)$ で求められます。 $w$ の値を二分探索することで、クエリあたり計算量 $O((\log N)^2)$ を達成します。
解説記事の類は見つかりませんでしたが、いくつかの提出がこの解法を用いています。
クエリ当たり $O(\log N)$ へ
まず問題の整理から行います。
兄弟が合流するのが最適な場合は、その判定も含めて LCA の計算と同様に計算量 $O( \log N)$ で処理できます。以下、兄弟が合流しないと仮定して計算します。このとき、兄弟が両方訪れる頂点を $2$ 重に数えてしまっても問題ありません。
マージ過程を表す木のノード $v$ の重みは、そのマージの要因となった辺の重み(無ければ $-1$ )とし、 $w(v)$ と表します。ノード $v$ の親を $p(v)$ (ない場合は $p(v):=v$ )と表します。ノード $v$ の $n$ 段階親を $p^n(v)$ と表します。ノード $v$ はいくつかの頂点がマージされた要素を表すので、その頂点数を $s(v)$ と表します。
例えば、任意のノード $a$ で
- $w(a) \lt w(p(a))$ または $a$ は根
- $s(a) \lt s(p(a))$ または $a$ は根
- $s(p^N(a))=N$
が成り立ちます。
頂点 $x$ からマージ過程を表す木上で親方向に進む回数を $A$ とし、頂点 $y$ からも同様に $B$ とします。適切な $(X,Y)=(p^A(x),p^B(y))$ の組を求めたいですが、対象ノード自身とその親についての関係を考えたいので、合計 $z$ 個のノードを訪れられるようになる直前の状態を求めることにします。
$X$ が $X^{\prime}=p(X)$ に移動するようなマージが起こる条件は、 $w(X^{\prime})\leq w(p(Y))$ です。 $1$ 回もマージされていないノードの重みを $-1$ に設定したことにより、初期状態も含め、実際のマージ過程に現れる組 $(X,Y)$ について
- $w(X) \leq w(p(Y))$
- $w(Y) \leq w(p(X))$
が成り立ちます。
また、合計 $z$ 個のノードを訪れる直前であるということから、
- $s(X)+s(Y) \lt z$
- $w(p(X)) \leq w(p(Y))$ ならば $z \leq s(p(X))+s(Y)$
- $w(p(Y)) \leq w(p(X))$ ならば $z \leq s(X)+s(p(Y))$
が成り立ちます。
数式だけでは理解しにくいので、下図を参考にするとよいです。 $w(p(X))$ と $w(p(Y))$ の比較はよって次にマージが進む向き(矢印)を導きます。実際に経由する状態は矢印が青の地点です。そのうち、 $s(X)+s(Y)\lt Z$ と $Z\leq s(X)+s(Y)$ の境界(折れ線)の手前の地点(丸で囲んだマス)が求めるものです。
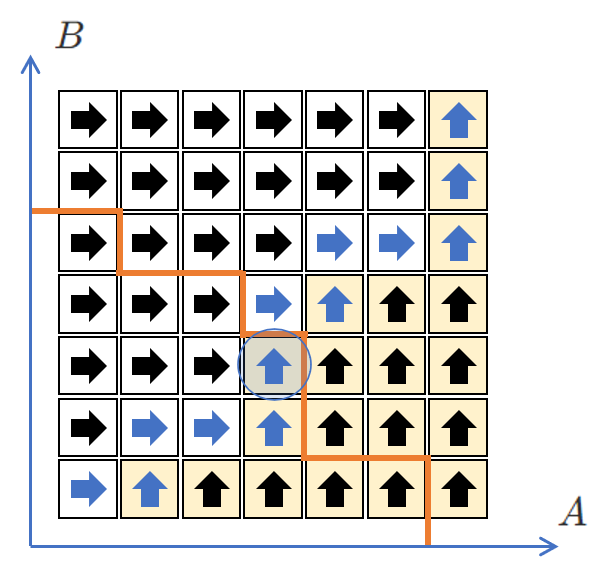
いま、 $0 \leq A \lt 2^{a+1}$ かつ $0 \leq B \lt 2^{b+1}$ $(0\leq a,b)$ に絞られているとします。次のように場合分けすることでそれぞれ結論が得られます。
- $z \leq s(p^{2^a}(x))+s(p^{2^b}(y))$ かつ $w(p^{2^a}(x)) \leq w(p^{2^b}(y))$ ならば、 $B \lt 2^b$
- $z \gt s(p^{2^a}(x))+s(p^{2^b}(y))$ かつ $w(p^{2^a}(x)) \leq w(p^{2^b}(y))$ ならば、 $2^a \leq A$
- $w(p^{2^a}(x)) \gt w(p^{2^b}(y))$ ならば、 $x,y$ を交換して(伴って $A,B,a,b$ も交換する) 1. , 2. に帰着
1. , 2. の場合において、条件から導かれる矢印(条件が直接導く矢印を青にします)や、折れ線と青矢印のマスの位置関係、および求めるマスが存在しうる領域(赤)を図で表すと次のようになります。
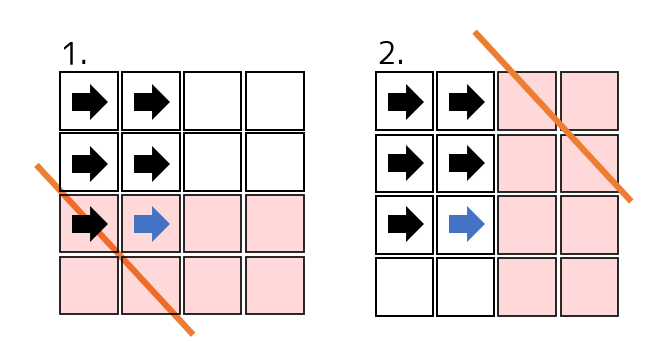
$A,B$ の下限が分かった場合は、 $x,y$ を根側に移動して $A,B$ の上限を狭めます。
どの場合も、探索する領域のいずれかの方向の幅が $\frac{1}{2}$ 倍になります。よって、 $O(\log N)$ 回繰り返す内に $A$ と $B$ どちらかの値が求まります。実際に計算するとき、 $p^{2^a}(x)$ などはダブリングのテーブルを参照することで計算量 $O(1)$ で計算でき、ほかの要素も各ノードについて前計算されていれば計算量 $O(1)$ で $1$ 回の繰り返しができます。
$A,B$ どちらかが求まれば単純な二分探索でもう一方が求まります。
$z$ 個の頂点を訪れられるようになる直前の状態が分かったので、その次に起こるマージにかかわる辺の重みが答えです。
以上より、クエリを計算量 $O(\log N)$ で処理できます。
解答例

線形時間の LCA,LA 解法を用いる場合の計算量
ダブリングのテーブルを構築するため現状 $\text{best}$ でも $\Theta (N \log N)$ の計算量および記憶域を使いますが、 LCA problem と level ancestor problem を線形時間+クエリ定数時間で解くアルゴリズムを使用するとテーブルは不要になります。全体の計算量は $O(N+M\alpha (N) + Q \log N)$ になります。
lowest common ancestor : cf. ジョイジョイジョイ https://joisino.hatenablog.com/entry/2017/08/13/210000
level ancestor : cf. 37zigenのHP https://37zigen.com/level-ancestor-problem/