まとまった内容ではありませんが、(コンテスト問題に対して解法解説とかをやらなくなったものあって)記事投稿頻度が減ったぶんの埋め合わせにしようと思います。
動機
(↑私の作問でも私の投稿でもありません)
問題概要
(原問題から簡略化しています)
正整数 $A$ , $B$ , $L$ , $R$ および文字列 $S$ , $T$ が与えられます。 $T$ は短く、 $S$ は長いものとします。 $T$ を $k$ 回繰り返した文字列を $T^k$ 、文字列 $X$ , $Y$ の編集距離(レーベンシュタイン距離) を $d(X,Y)$ と表すとき、次の値を求めてください。
$$\max_{L\leq k\leq R, k\in\mathbb{Z}}Ak-Bd(S,T^k)$$
メインの主張
$S$ , $T$ を文字列とします。このとき次で定義する上三角行列 ( $0\leq l\leq r\leq |S|$ について、 $(i,j)$ 要素を $A_{l,r}$ とします) は Monge です。
- $A_{l,r}$ の値を $S[l..r)$ と $T$ の編集距離とします。ただし、
- $S[l..r)$ は $S=S_0S_1\ldots S_{|S|-1}$ の部分文字列 $S_lS_{l+1}\ldots S_{r-1}$ です。
- 「編集距離」はレーベンシュタイン距離を指します。挿入/削除/置換のコストはそれぞれ $1$ とします。
証明
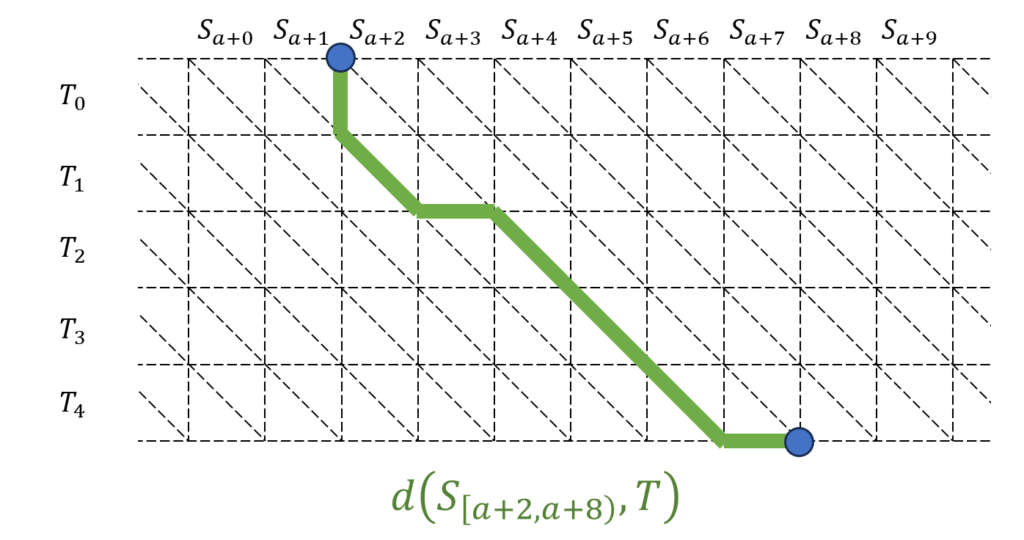
文字列 $X$ , $Y$ の編集距離は、あるグラフの最短距離に帰着することで $O(|X||Y|)$ 時間で計算できます。特に、このグラフは平面グラフです。さらに、片方がある文字列の部分文字列として動く場合、編集距離は帯状のグラフを横切るような経路の最短距離が対応します(図)。
Monge 性の四角不等式に対応するパスを考えます。不等号を $\geq$ としたときの左辺に対応する $2$ つのパスのうち、コストの最小値を達成するものをとります。グラフ全体が平面グラフであることと、始点終点の位置関係より、この $2$ つのパスはある頂点で交差します。よって、コストの和を変えずに始点終点の組を変えることができて、そうすると右辺に対応するパスが得られます(図)。よって、四角不等式が成立し、上三角行列の Monge 性が示されました。
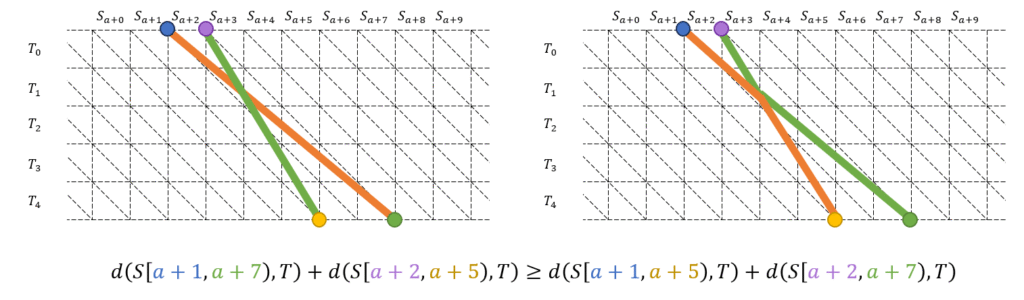
アプローチ
まず $S[l..r)$ と $T$ の編集距離をオンラインクエリとして高速に求められるようにします。編集過程で $T$ をどのように得るかは、 $T$ の各文字それぞれをどのように得るか $3$ 通り( $S$ の文字を残す / $S$ の文字を書き換える / 挿入する)を考えれば、 $3^{|T|}$ 通りに分けられます。それぞれが実行可能かどうかは、 $S[l,r)$ から貪欲に取り出せば判定でき、適切な前計算のもとで $1$ 文字あたり $O(1)$ 時間で判定できます。この貪欲法の過程でコストが等しいものをまとめることで $O(|T|^2)$ 時間の動的計画法を得ます。これで $S[l..r)$ と $T$ の編集距離を $O(|T|^2)$ 時間で求められます。
$S$ を $k$ 個の部分文字列に分割してそれぞれ $T$ との編集距離をとったものの総和を考え、すべての分割方法についてその最小値をとれば、 $S$ と $T^k$ の編集距離に一致します。もし、分割後の文字列に空文字列を許さなければ、単に $k$ を固定した最大化問題は Mongeグラフ上の $k$-辺最短路問題です。
$k$ の範囲を制約せず、空文字列への分割を許さないとする場合の解は、 LARSCH 法を用いれば $O(|S|)$ 回のクエリで求められます。
最適解が空文字列を含む場合、 $k=M$ で、分割後の空でない文字列の個数 $k^\prime$ は $-Bd(S,T^{k^\prime})+B|T|{k^\prime}$ の値を最大化します。このような $k^\prime$ も $O(|S|)$ 回のクエリで求められます。
これらが $k$ の範囲の制約を満たさない場合、解は範囲の境界にあって、かつ空文字列を含まない分割になります。これは $k$ を固定した問題を考えれば、 $O(|S|\log (|S||T|AB))$ 回のクエリで答えられます。