まとめブログ。
傲慢になって用語を定義してしまおうという部分と、調査記録のような部分があります。
- DP とは
- お約束
- DP の俗称
- 部分和 DP
- ナップサック DP （ナップザック DP ）
- ゲーム DP
- 区間 DP
- bit DP
- 3^n の DP （ O(3^n) の DP 、部分集合 DP ）
- 貰う DP
- 配る DP
- 木 DP
- 2 乗の木 DP 、 O(NK) の木 DP
- 全方位木 DP （ Rerooting DP ）
- 部分列 DP
- $d$ 次元 DP
- in-place DP （インライン DP ）
- 戻す DP
- 桁 DP 、 竹 DP
- 耳 DP （状態 DP ）、 chokudai DP
- 挿入 DP
- 箱根駅伝 DP （箱根 DP ）
- Lucy DP
- 連結性 DP （連結 DP ）・ フロンティア法
- Alien DP （ Aliens DP ）
- 重軽再帰動的計画法（ HLRecDP ）
- 座布団 DP
- その他
- 参考サイト（全般）
DP とは
動的計画法は英語で dynamic programming であり、 DP と略されます。競プロにおける動的計画法とは、人によって範囲が曖昧であるところ(*1)ですが、ここでは便宜的に「本問題（解くべき問題）に対して、サイズの小さい可変個の小問題を設定し、適切な順番に解くことで本問題を解く方法」と定義します。
可変個の小問題の解は、本問題や上位の小問題の解の計算に利用されるので、テーブルという配列に保存する必要があります。このための配列の変数名を dp とする慣習があります。これによる見やすさのため本記事では $\text{dp}[a][b][ \ldots ]=$ ( $a,b,\ldots$ に関する小問題の解 ) という表記で小問題を定義します。
ところで、競プロ界隈の情報共有では、解法に表れた DP の特徴に応じたさまざまな名前が使われています。これにより、典型的な DP の理解に役立つほか、（例えば、 $\mathbb{X}$ (旧 Twitter) の文字数制限に対応するための）文字数削減に役立ちます。
(*1) see also DPの話 – aizuzia DPはDAG上の最短経路ではない – うさぎ小屋
お約束
もし異なる解釈を知っている場合や、名称の定義の根拠を提供いただける場合で、それを報告いただければ修正または追記する場合があります。
DP の俗称
部分和 DP
部分和 DP とは、部分和問題を解くための DP のことです。部分和問題とは、次のような問題です。
非負整数列 $A=(a_1,a_2,\ldots ,a_N)$ と非負整数 $S$ が与えられる。
要素の組み合わせ（ = 添え字の集合） $\lbrace k_1,k_2,\ldots ,k_K \rbrace$ であって $a_{k_1}+a_{k_2}+\cdots +a_{k_K}=S$ となるようなものは存在するか？
具体的には次のように小問題をおいた DP を部分和 DP といいます。
$\text{dp}[ n ][ s ] =$ ( $A=(a_1,a_2,\ldots ,a_n), S=s$ としたときの部分和問題の解 )
$(0 \leq n \leq N , 0 \leq s \leq S)$
このテーブルの要素は真偽値であるため、ここに追加情報を持たせる拡張を考えることができます。また、拡張しない場合はビット演算によって省メモリ化・高速化できます。
ナップサック DP （ナップザック DP ）
ナップサック DP とは、ナップサック問題を解くための DP のことです。ナップサック問題とは、次のような問題です。
- $1 \leq i \leq N$ について、重さ $w_i$ と価値 $v_i$ （それぞれ非負整数）の組
- 非負整数 $W$
が与えられます。
要素の組み合わせ（ = 添え字の集合） $\lbrace k_1,k_2,\ldots ,k_K \rbrace$ であって、重みの総和が $W$ 以下つまり $w_{k_1}+w_{k_2}+\cdots +w_{k_K}\leq W$ のとき、価値の総和 $v_{k_1}+v_{k_2}+\cdots +v_{k_K}$ の最大値を求めよ。
ナップザック問題は NP 困難に属する有名な問題ですが、さまざまな制約に対してそれぞれ効率的な解法があります。具体的なものについては、 AOJ コースを参照してください。
EDPC D EDPC E TDPC H AOJ コース 組み合わせ最適化
ゲーム DP
ゲームについて、互いに最適に操作した場合の勝敗および利得をミニマックス法等で求める DP をゲーム DP といいます。(*1) Grundy 数を求める場合も DP が使えますが、こちらがゲーム DP と呼ばれることは少ないようです。(*2)
二人零和有限確定完全情報ゲーム(Wikipedia)は、到達可能な局面全体が有限 DAG をなすので、そのまま DP で各プレイヤーの利得が求まります。一般的にはミニマックス法、また特殊なものはネガマックス法とも呼ばれます。
$\text{dp}[ s ] =$ ( $s$ を初期盤面としてゲームをした場合の結果 )
$($ $s$ は本問題の初期盤面から到達可能 $)$
(*1) ref. (RANDOM) (けんちょんの競プロ精進記録)
(*2) 単に「 Grundy 数を計算する」と言われています。
区間 DP
長さ $N$ の列があったとすると、その連続部分列すべてを計算対象とするような DP を区間 DP といいます。例えば列 $A=(a_1,a_2,\ldots ,a_N)$ に関する本問題の小問題は次のように設定します。
$\text{dp}[l][r]=$ ( $l,r$ に関して、特に $(a_l,a_{l+1},\ldots ,a_{r-1})$ に関して設定した小問題の解 )
$(1\leq l\lt r\leq N+1)$
さらに例えば、長さ $1$ の連続部分列を初期条件として、しだいに長い連続部分列に対して計算し、最終的に列全体の計算結果が得られるというパターンがあります。
bit DP
ある小さい集合の部分集合をテーブルの添字とするような DP は bit DP と呼ばれます。つまり、集合 $A=\lbrace a_1, a_2, \ldots ,a_N \rbrace$ に関する本問題の小問題は次のように設定されます。
$\text{dp}[B]=$ ( 集合 $B$ に対して設定した小問題の解 )
$(B\subset A)$
このような DP では、部分集合を bit 列として整数型変数 $1$ 個で表現することがほとんどです。
(参考) アルゴリズムロジック , けんちょん@Qiita
3^n の DP （ O(3^n) の DP 、部分集合 DP ）
集合 $A$ の上の bit DP であって、 $\text{dp}[B]$ $(B\subset A)$ を計算する際に $C\subsetneq B$ となる $C$ を列挙して参照しなければならないとき、全体の参照回数はおよそ $3^{|A|}$ となります。
このような DP は「 $O(3^n)$ の DP 」または「部分集合 DP」と呼ばれます。
実装方法は他の記事を参考にしてください。
貰う DP
計算が完了していない領域を現状態として注目し、計算が完了している領域の結果から現状態を計算するように実装された DP のことを貰う DP と呼ぶことがあります。
漸化式で設計した DP を直接実装すると、貰う DP になります。
(参考) 配る DP・もらう DP の特徴づけに関して | えびちゃんの日記
配る DP
計算が完了している領域を現状態として注目し、まだ完了していない領域への寄与を計算するように実装された DP のことを配る DP と呼ぶことがあります。
今の状態の次はどのような状態になりうるか？という状態遷移の考えで設計した DP を直接実装すると、配る DP になります。
木 DP
根付き木 $T$ に関する問題があるとき、次の小問題を設定します。
$\text{dp}[v]=$ ( 頂点 $v$ に関する問題の解 )
この問題はしばしば頂点 $v$ の部分木に関する本問題です。ここで頂点 $v$ の部分木とは、頂点集合が $T$ における $v$ の子孫であり、根が $v$ であるような $T$ の根付き部分木のことです。
根付き木を葉から根に向かう方向（ボトムアップ）、あるいは根から葉に向かう方向（トップダウン）のどちらか一方のみに走査する DP は木 DP と呼ばれます。
2 乗の木 DP 、 O(NK) の木 DP
対象の根付き木の頂点数を $n$ とします。各頂点にはサイズ $1$ のデータがあるとします。
木 DP の $1$ ステップにおける計算量が部分木のサイズに依存する場合を考えます。頂点 $v$ の子が持っているデータを合併してひとまとめにしますが、ここではデータ $2$ 個を $1$ 個にまとめることを繰り返すことで処理することを仮定します。
(1) サイズ $a$ のデータとサイズ $b$ のデータを合併すると、計算量が $O(ab)$ だけかかってサイズ $a+b$ のデータが得られるとき、木 DP の計算量は $O(N^2)$ になります。この計算量解析を利用した DP は $2$ 乗の木 DP と呼ばれます。
(2) サイズ $a$ のデータとサイズ $b$ のデータを合併すると、計算量が $O(ab)$ だけかかってサイズ $\min (a+b,K)$ のデータが得られるとき、木 DP の計算量は $O(NK)$ になります。この計算量解析を利用した DP は $O(NK)$ の木 DP と呼ばれます。
(参考) あなたは嘘つきですかと聞かれたら「YES」と答えるブログ
全方位木 DP （ Rerooting DP ）
ボトムアップの木 DP の結果を任意の根に対して一度に計算するような DP は全方位木 DP と呼ばれます。
葉から根に向けて木 DP を計算したのち、各頂点 $v$ について、 $v$ の子を一列に並べて双方向に累積を計算しておくと、根から葉に向かう順序で木 DP と同様の集約が頂点あたり定数回のマージで実現されます。
定式化の方針が多様・複雑なので、実例のリンクの列挙に留めます。
- アルゴリズムロジック（頂点・辺ラベルを無視したシンプルな定式化。）
- 【全方位木DP】明日使える便利な木構造のアルゴリズム keymoon@Qiita（モノイドの可換性を要求しない。）
- 抽象化全方位木DPのライブラリとドキュメント noya2@traP（複数の概念に言及する詳しい定式化。）
部分列 DP
ある列の（連続とは限らない）部分列全体を重複を除いて処理するための特徴的な DP は部分列 DP と呼ばれます。
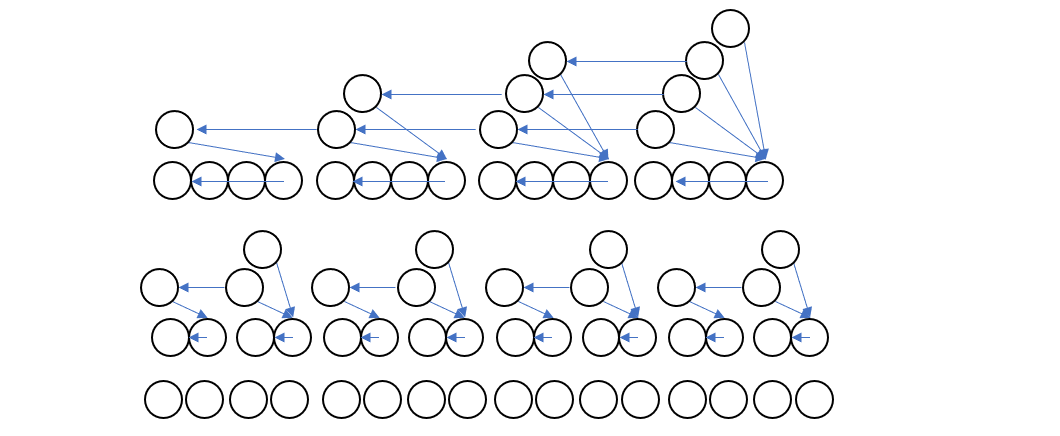
整数列 $A=(a_1,a_2,\ldots ,a_N)$ の部分列として得られる数列に対して、その取り出し方を先頭に近い要素から貪欲に採用することを考えます。このような規則のもとでは、 $i$ 番目の要素が選ばれる場合の直前の要素としてあり得るものを考えると、 $i$ 番目よりも前にあって値が $a_i$ と等しい要素が
- 存在しないなら、すべての要素は直前になり得ます。また、
- 存在する場合、そのような要素のうち最も後にくるものの要素番号を $j$ とすると、直前の要素の要素番号は $j$ 以上です。
よって、次のようなテーブルで DP をすれば都合がよいことがわかります。
$\text{dp}[j][i] = $ (最後に取り出した要素の番号が $j$ 以上 $i$ 以下であるような部分列に関する小問題の解)(*1)
$(1\leq j\leq i\leq N)$
参考： AtCoder 公式解説
小問題の設定のしかたは他にもありますが、いずれも部分列を重複して数えるのを防ぐ工夫があるため、部分列 DP と呼ばれます。
(*1) これは区間集約クエリなので実際は $1$ 次元で十分でありがちです。
$d$ 次元 DP
$d$ には具体的な正整数が入ります。
$d$ 次元配列を使用する DP です。（どちらかというと） in-place 化によって除かれる前の次元を数えます。
in-place DP （インライン DP ）
一部の更新を in-place にするという工夫を行った DP のことです。「 in-place 化した DP 」の略記であるとみなしたほうがよいかもしれません。
適切な in-place 化により、
- 計算途中の情報をすべて保存することによるメモリの圧迫の軽減、
- 一部計算を省略することによる高速化、可読性の向上
が発生することがあります。
戻す DP
DP を完全に計算したあと、部分的に、本来の DP とは逆の手順を行うことで目的を達成するような解法を「戻す DP 」と呼びます。
例えば、次のような問題に有効です。
正整数 $N$ , $M$ および、正整数の列 $A = (A_0,A_1,\ldots ,A_{N-1})$ が与えられます。 $\sum_{i=0}^{N-1}A _ i = M$ です。 $i = 0,1,\ldots ,N-1$ および $x = 1,2, \ldots ,M$ について、 $A$ から $i$ 番目の要素のみを取り除いた列を $B_i$ としたとき、$B_i$ の（連続とは限らない）部分列の取り出し方であって、要素の総和が $x$ となるようなものの個数を $998\, 244\, 353$ で割った余りを求めよ。
$A$ 全体に対して計算した後に任意の要素を取り除くような意味の計算ができるため、 $O(NM)$ ステップの計算ですべての答えが求まります。
桁 DP 、 竹 DP
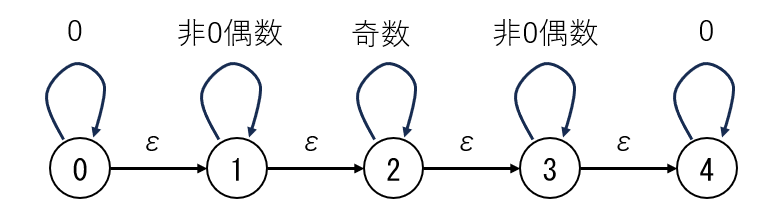
$N$ 桁以下の非負整数 $x$ 全体にわたる計算をするとき、次のようなテーブルを用いた DP が有効な場合がありますが、それを桁 DP といいます。
$\text{dp}[ n ][ c ]=$ ( $x$ の上位 $n$ 桁まで確定させ、その部分について特定の値との大小関係が $c$ で表されるようなものに対する小問題の解 )
同様に、値として意味がある整数を桁ごとに見ることで高速な DP を設計できる場合、それが桁 DP と呼ばれます。
一方で、下位から確定させてゆく種類の桁 DP が使われる場合もあります。
$\text{dp}[ n ][ c ]=$ ( $x$ の下位 $n$ 桁まで確定させ、その部分について特定の値との大小関係が $c$ で表されるようなものに対する小問題の解 )
これは、前者の桁 DP （けた DP ）とは逆向きであることから竹 DP （たけ DP ）と呼ばれることがあります。
EDPC S TDPC E 例題(JOI/AtCoder) 例題(AtCoder) 例題(AtCoder)
耳 DP （状態 DP ）、 chokudai DP
「名前の対象範囲が人によって異なるもの」としても有名です。
素晴らしい問題のネタバレになるおそれがあるため、以下の説明は畳んでおきます。
AtCoder 「みんなのプロコン 2019」 D – Ears の類似は「耳 DP 」と呼ばれることがあります。一方で、「耳 DP 」と捉えられる範囲は明確ではなく、個人差が明らかです(*1)(*2)。
実行可能な配列の条件を整理して、各点に適用されうる基本条件（ $1$ つの耳における調整前の石の個数）を列挙したとき、許容される基本条件の切り替わりの様子をちょうど受理するような有限オートマトンを構築できます。Ears の解法はこれを利用した DP です。この有限オートマトンは絶妙に見出しにくく、考察したときに他の方針に誘導されやすいという特徴があります。
$\text{dp}[i][p]=$ ( 列を $i$ 項まで読み込んだときにオートマトンの状態 $p$ に至る場合に関する小問題の解 )
$0\leq i \leq N, p\in \lbrace 0,1,2,3,4 \rbrace$
また、耳 DP と呼ばれる(*3)ものであって出題頻度が高いタイプの出題例として、 ABC211C – chokudai も紹介します。こちらのほうが簡単な問題であり目に触れやすく、競プロ典型90問での出題もあり、むしろこちらのほうが耳 DP の核だと考えるほうが多数派かもしれません。
また、特にこのパターンの DP を chokudai DP と呼ぶことがあります。(*4)
(*1) (a) noimi_kyopro@$\mathbb{X}$ 「ぼくは Ears をあんまり耳DP の代表例だと思ってないです」・ (b) drken1215@$\mathbb{X}$ 「dp[ i ][ 状態 ] な DP をするときに、状態の変化が「Phase を進める」という解釈ができるものが耳 DP というイメージ。」 と言及される。 (b) は Ears を含む意図を見いだせる、 (a) とは異なる解釈である。
(*2) chokudai@$\mathbb{X}$ 「……指す範囲が人によって異なり、「耳DPで解ける」といっても通じない事が多いので、正直使用については非推奨です。」
(*3) 競プロ典型90問 E869120(@$\mathbb{X}$) (@GitHub)
(*4) heno239@$\mathbb{X}$ (発案？) , chokudai@$\mathbb{X}$
挿入 DP
列 $A$ の並べ替え全体について計算するとき、
$\text{dp} [ i ] = $ ( 列 $A$ の先頭 $i$ 項の並べ替え後の前後関係を決定した状態に関する小問題の解 )
として $i$ の昇順に計算することが考えられます。これは、まず空列 $B$ があって、列 $A$ の要素を順に取り出しながら $B$ の任意位置に挿入することで $A$ の並べ替えを $B$ に構築する手順を表します。このような DP は挿入 DP と呼ばれます。
隣接項について制約がある場合、制約を満たさないような隣接箇所の個数の情報を添え字に持ちながら計算するパターンがあります。
EDPC T TDPC O 出題例(AtCoder) 出題例(JOI/AtCoder)
箱根駅伝 DP （箱根 DP ）
$0\leq A_1\leq A_2\leq\cdots\leq A_N\leq N$ となる広義単調増加列が与えられたうえで、整数列 $(1,2,\ldots ,N)$ の並び替え $(p_1,p_2,\ldots ,p_N)$ 全体に対して集約したいときに使用され、次のようなテーブルを用いる DP を箱根駅伝 DP と呼びます。
$\text{dp}[m][k] = $ （組 $(i,p_i)$ のうち $i \leq m$ かつ $p_i \leq A_m$ を満たすようなものが $k$ 個であるような場合に対して設定した小問題の解）
$(0\leq k\leq m\leq N)$
たいていは $A_i=i$ であり、つまり次のようなシンプルな形です。(*1)
$\text{dp}[ m ][ k ] = $ （組 $(i,p_i)$ のうち $i \leq m$ かつ $p_i \leq m$ を満たすようなものが $k$ 個であるような場合に対して設定した小問題の解）
$(0\leq k\leq m\leq N)$
箱根駅伝とは、 ICPC 2012 夏合宿の 3 日目 F の問題(*2)のことです。その問題の講評で箱根駅伝 DP による解法が言及されています。
(*1) 出題例および解説ブログではたいていシンプルな方のみが扱われていますが、 AtCoder の某問題の公式解説が拡張された解釈を示したため本投稿ではこのようにしました。
(*2) 参考： けんちょんの競プロ精進記録
Lucy DP
Lucy DP とは、 $N$ 以下の素数の個数、あるいは $N$ 以下の素数の総和のような対象を計算したいときに、 $n=\text{floor}(\frac{N}{k})$ $(1 \leq k \leq N, k\in\mathbb{Z})$ としてありうる $n$ について小問題を設定することで得られる、 $\tilde{O}(N^{\frac{3}{4}})$ (*1)あるいは $\tilde{O}(N^{\frac{2}{3}})$ という特徴的な計算量をもつ DP です。
由来は Project Euler における Lucy_Hedgehog の投稿です。(*2) アルゴリズムを理解したければえびちゃんによる資料 (*3) を参考にするのがよさそうです。(*4)
乗法的関数の prefix sum を管理して Dirichlet 積に関係する演算を行うアルゴリズム(*5)でも特徴的な計算量が現れますが、これは Lucy DP とは呼ばれません。
(*1) ここでは、 $\tilde{O}$ 表記は $O$ 表記において $\log N$ の定数乗による差を無視したものとします。
(*2) Project Euler に登録し、 10 番の問題を解くことで閲覧できるようになります。私は閲覧しました。
(*3) 参考 : 眠れない夜は素数の個数でも数えましょう – えびちゃんの日記 , 素数の数え上げと乗法的関数の和 – えびちゃん (rsk0315)
(*4) 他にも解説していそうな記事を列挙しておきます。 (griff’s math blog!) (math314) (Sugarknri) (Suu) (TKO)
(*5) 参考 : Dirichlet 積と、数論関数の累積和 | maspyのHP
連結性 DP （連結 DP ）・ フロンティア法
$N\times M$ のマス目から $1$ つ以上のマスを選び、それが連結であるようにしたとします。ここで、連結であるとは、辺を共有するマスに移動することを繰り返すと、選んだマスのどの $2$ つであっても選んだマスのみを通って行き来できることをいいます。
穴の開いた形や渦巻きのような形も対象になるので、 $N$ も $M$ も大きければこのような形の列挙は困難です。ただし、 $N$ が非常に小さければ、走査によって現実的な DP が可能です。そのためにはまず、すでに走査された部分によって走査線にかかるマスの連結状況としてありうるものを列挙しなければなりません。そのため、シンプルな走査であるという理論に対して実装は大変です。
あくまで具体例ですが、小問題の設計方法は次のようなものがあります。
$\text{dp}[m][S]=$ (走査線にかかる $N$ 個のマスを $(0,1,2,\ldots ,N)$ とし、選ばれたものを連結成分に分けたとき $S=\lbrace s_0,s_1,\ldots ,s_{k} \rbrace$ （ $s_i$ は $\lbrace 0,1,2,\ldots ,N\rbrace $ の部分集合） となる場合について適切に設定した小問題の、 $N=m$ のときの解。 )
$(0\leq m \leq M, i\neq j \implies s_i \cap s_j=\varnothing )$
TDPC S 出題例(AtCoder) 出題例(yukicoder)
Alien DP （ Aliens DP ）
制約付き最適化問題に対してラグランジュ緩和問題を利用する発想を Alien DP と呼ぶことがあります。(*1)
ほとんどは Monge グラフ上の $d$-辺最短路問題として出題されます。
名前の由来は IOI 2016 – Aliens (JOIのサイト) です。
(*1) ア辞典のページ より引用。理論はそちらを参照すること。
(参考) 出題例(AtCoder) の公式解説
重軽再帰動的計画法（ HLRecDP ）
new : 2023/11/08
俗称というよりは、論文で定義された、通用する(であろう)用語です。(*1)
重軽再帰動的計画法 (heavy-light recursive dynamic programming) は、 [1] 木上のナップサック問題 Qiita@tmaehara で紹介されたアルゴリズムです。根付き木上で定義される制約付きナップサック問題の解法の一つです。
(*1) よって、公開されている論文を見ると正確な定義が書かれています。
(*2) どのような条件ならアルゴリズムが成立するのかは、このアルゴリズムが提案された論文を参照してください。
座布団 DP
素晴らしい問題のネタバレになるおそれがあるため、以下の説明は畳んでおきます。
その他
用例は確認したが、取り立てて説明する必要がないと判断したもの。
- 確率 DP 、期待値 DP : 本問題や小問題が確率、期待値を求める問題であるような DP 。
- 再帰 DP 、メモ化再帰 : 再帰関数で実装する DP 。メモ化した再帰関数のこと。
- Monge DP：行列の Monge 性を利用する DP 。モンジュと読む。
- オフライン DP 、オンライン DP : 動的計画法高速化テクニック（オフライン・オンライン変換） tmaehara@Qiita
- chokudai DP : 耳 DP (*4) を参照。
- 文字列 DP : AtCoder Tags にカテゴリがある。文字列が主役の問題で解法が DP でさえあればそう呼ばれるのではないだろうか？
- Sum over Subsets DP （ SOS DP ） : (USACO Guideより。) いわゆる高速ゼータ変換。
- 連続 DP : 俗称というわけではなく、用語が存在する。
よく分からなかったもの。
参考サイト（全般）
AtCoder Tags 有志によって AtCoder の問題の分類がなされます。特に、分類にはタグ名がついています。
はまやんはまやんはまやん hamayanhamayan による膨大なブログです。競プロ問題のカテゴリ化専用の記事もあります。
Kyopro Encyclopedia of Algorithms (ア辞典) なんと査読がついている
$\mathbb{X}$ (旧 Twitter) みんなだいすき