マージ過程を表す木の高さが $O( \log n)$ であるとき、重要な性質を失わずに二分木に変形できます。
2022/09/01 に全体を更新しました。古いバージョンの pdf が欲しい場合は連絡をいただけると送るかも?
基本テクニック
マージ過程を表す木
いくつかの要素が $1$ つになるまでマージされる過程を根付き木で表します。
まず初期状態の要素ごとに頂点を作成します。 $n$ $(1 \leq n)$ 個の要素をマージするときは新しい頂点 $p$ を作成し、もとの要素に対応する $n$ 個の頂点は $p$ の子とします。要素が $1$ 個になるまでマージを繰り返して得られた根付き木を、マージ過程を表す木と呼びます。
マージテク $\text{A}$
サイズ $a$ の要素とサイズ $b$ の要素をマージすると、コスト $a+b$ がかかり、サイズ $a+b$ の要素を得ます。各要素のサイズが $1$ 以上、合計サイズが $n$ の要素たちが一列に並んでいます。要素が $1$ 個になるまで、隣り合う $2$ つの要素を好きに選んでそれらをマージした要素で置き換えることを繰り返すとき、コストの総和を $O(n \log n)$ とする方法があります。(この事実を マージテク $\text{A}$ と呼ぶことにします。)
マージの逆の、分割の過程を考えます。列の左端からサイズの累積和が $\frac{n}{2}$ となる地点を占める要素を $m$ とします。 $m$ の両側で分割すると、次の $3$ つの部分に分かれます。
- $m$ よりも左側の、サイズの総和が $n/2$ 以下の部分
- $m$
- $m$ よりも右側の、サイズの総和が $n/2$ 以下の部分
この分割を再帰的に行います。分割の逆に従ってマージすると、大きさ $x$ の要素がマージに巻き込まれる回数は高々 $2+2 \lfloor\log_2 \frac{n}{x} \rfloor$ です。
よって、コストの総和は $2n (\lfloor \log_2 n \rfloor + 1)$ であり、マージテク $\text{A}$が示されました。
特に、 $2+2 \lfloor\log_2 \frac{n}{x} \rfloor$ を後の計算量解析で利用します。
備考(*2)
マージテク $\text{A2}$
マージテク $\text{A}$ で、列に関係なく任意の $2$ 要素の組を選んでマージできるとき、 小さい順に $2$ つの要素をマージすることを繰り返します。
はじめの大きさが $a_0$ である要素がマージに巻き込まれて至るサイズを順に $a_0,a_1,a_2, \ldots$ とします。 サイズが $a$ と $b$ の要素がマージされるなら一連のマージで $a \lt c \lt b$ であるようなサイズ $c$ の要素は現れないので、 $a_{i+2}-a_{i+1} \lt a_i \lt a_{i+1}$ が否定されます。 $a_i \lt a_{i+1}$ が明らかなので、 $a_i+a_{i+1} \leq a_{i+2}$ が導かれます。
以上より、 $(F_0,F_1,F_2, \ldots )=(1,1,2,3,5,8, \ldots)$ として $F_na_0 \leq a_n$ が成り立ちます。従って、大きさ $x$ の要素がマージに巻き込まれる回数は高々 $1+\lfloor\log_{\phi} \frac{n}{x} \rfloor$ $( \leq1+\lfloor 1.45\log_{2} \frac{n}{x} \rfloor)$ です。
記事の続きでは、マージに巻き込まれる回数の上限として次の評価も使います。
- $1+2\lfloor \log_{2} \frac{n}{x} \rfloor$
- $2 \leq \frac{n}{x}$ のとき、 $\lfloor 2\log_{2} \frac{n}{x} \rfloor$
マージテク $\text{B}$
このテクニックは記事中で使われません。
サイズ $a$ の要素とサイズ $b$ の要素をマージすると、コスト $\min \lbrace a,b \rbrace$ がかかり、サイズ $a+b$ の要素を得ます。各要素のサイズが $1$ 以上、合計サイズが $n$ の要素たちをどのような順序でマージしても、コストの総和は $O(n \log n)$ です。(一般的に Weighted Union Heuristic と呼ばれるこの事実を マージテク $\text{B}$ と呼ぶことにします。)
サイズ $a$ とサイズ $b$ の要素をマージするとき、コストに寄与する要素、つまり大きくない要素を $1$ つ選んでマークを付けます。マークが付けられた要素がマージされるときは大きさが $2$ 倍以上になるので、初期状態の各要素がコストに寄与するのは高々 $\lfloor \log_2 n \rfloor$ 回です。よって、コストの総和は $n \lfloor \log_2 n \rfloor$ であり、マージテク $\text{B}$ が示されました。
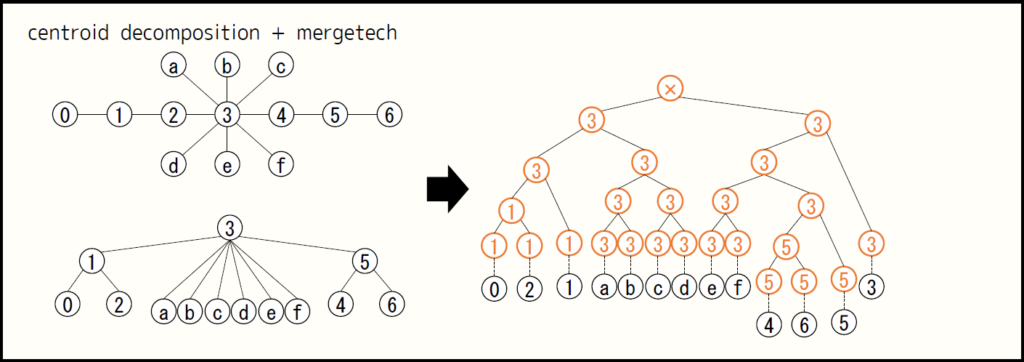
木の重心分解
木の重心にあたる頂点を除いて部分木に分割することを繰り返します。 $1$ 回分割すると各部分木の頂点数が $\frac{1}{2}$ 倍以下になるので、この分割を遡って得るマージ過程を表す木の高さは元の木の頂点数を $n$ として高々 $\lfloor \log_2 n \rfloor$ です。
木 $T$ が重心分解で重心 $g$ 、部分木 $t_0,t_1,\ldots ,t_k$ に分割されたとき、例えば木 $t_0$ に含まれる頂点 $u$ と木 $t_1$ に含まれる頂点 $v$ について、木 $T$ 上で $u,v$ 間の単純パスは重心 $g$ を通ります。この性質を用いて木の $\frac{n(n-1)}{2}$ 個の単純パスをマージ過程を表す木上の lowest common ancestor で分類し、計算を高速化する方法があります。特に、単純パスが $g$ を通るので、 $u,v$ 間の距離を $u,g$ 間と $v,g$ 間に分割できるのが重要です。
- 例:木上の等高線集約クエリ https://suisen-kyopro.hatenablog.com/entry/2022/03/21/220009
- 例:木上の距離に依存する数え上げ https://www.mathenachia.blog/tree-coulomb/
heavy light decomposition
根付き木を heavy path に分解し、高さ $O( \log n)$ の補助的な木に変形します。
根が唯一の頂点なら、それを heavy path にして終了です。根でいくつかの部分木に分割されるとき、最も大きい部分木を $1$ つ選んで $S$ とし、 $S$ の根と全体の根を heavy edge で結びます。それ以外の根の子は、根と light edge で結びます。これをそれぞれの子について再帰的に行います。
light edge を通って根に向かって進むと、部分木の大きさが必ず $2$ 倍以上になるため、任意の頂点から根までの単純パスが含む light edge の個数は高々 $\lfloor \log_2 n \rfloor$ です。
元の木から heavy edge を縮約すると、高さ $O( \log n )$ の根付き木が得られます。
各辺に頂点を $1$ 個挟んでから分解すると、元の木の辺に情報を乗せて heavy light decomposition ができます。
マージテク $\text{A}$ と高さ $O( \log n)$ のマージ過程との融合
重心分解との融合
木において、距離がある値以下の頂点に対するクエリ(木上の等高線集約クエリ)を、重心分解を用いて処理する方法があります。
参考文献:
重心分解のマージ過程を表す木は多分木ですが、各マージでマージテク $\text{A2}$ を用いると二分木(重心も $1$ つの部分木とみなすと、葉木)に変換されます。ある頂点を重心とするノードは重心分解で高々 $\lfloor \log_2 n \rfloor$ 回のマージに巻き込まれますが、その各段階で $2 \leq \frac{n}{x}$ のマージテク $\text{A2}$ を行っても高々 $\lfloor 2 \log_2 n \rfloor$ 回とでき、マージ過程を表す木の高さは $O( \log n)$ に保たれます。
マージ過程を表す木の各ノードでは、元の木の頂点を頂点 $g$ からの距離の昇順に並べたものと、そのテーブルで距離が変わる地点を管理します。ここで、 $g$ は、その部分木が重心分解で次にマージされるときの重心です。
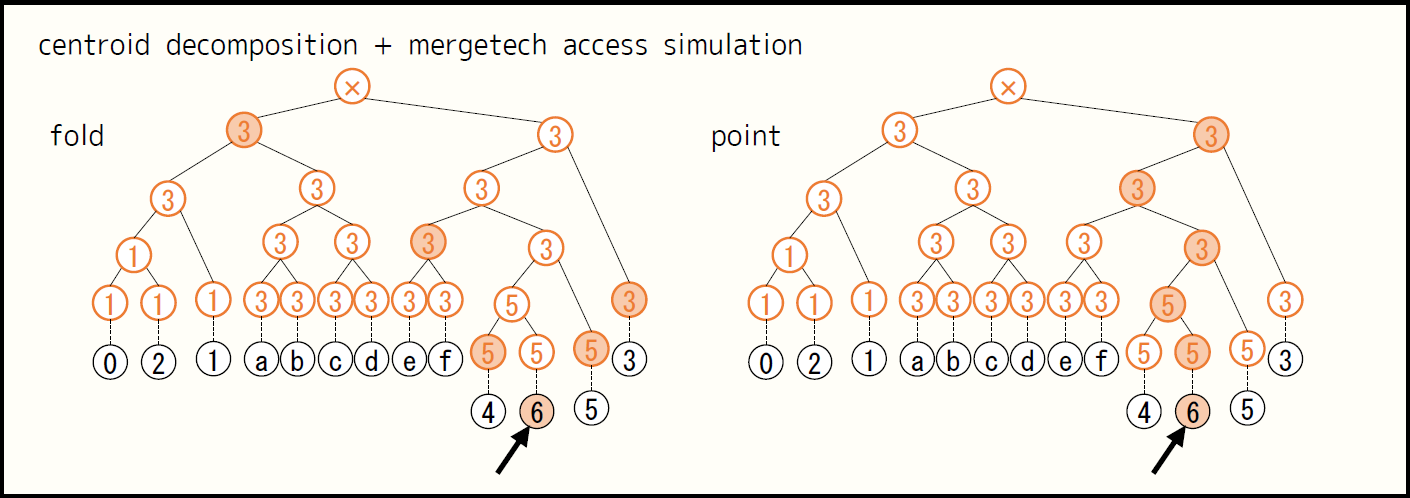
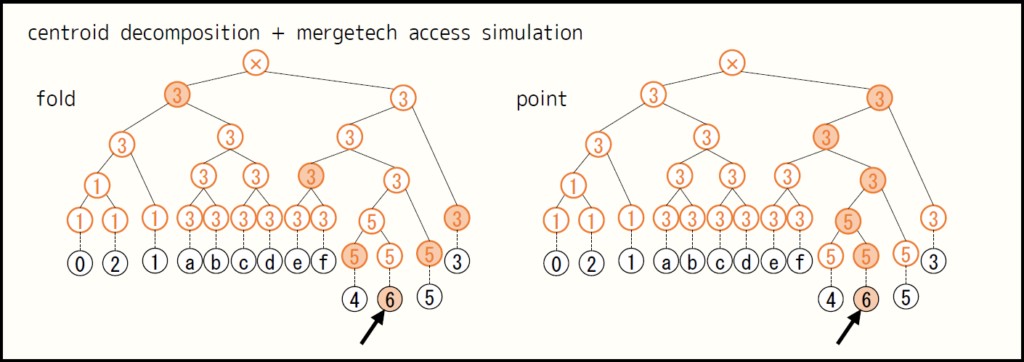
頂点 $v$ から距離が $l$ 以上 $r$ 未満であるような頂点をちょうど $1$ 回ずつ含む $O( \log n)$ 個の区間を得るためには、次のようにします。
- 頂点 $v$ からマージ過程を表す木の根までのパスを見る。
- 1. のパスに隣接する頂点で 1. のパスに含まれないノードについて、 $g$ からの距離が $l-\text{dist}(g,v)$ 以上 $r-\text{dist}(g,v)$ 未満であることに対応する区間を採用する。
- $l \leq 0 \lt r$ のとき、頂点 $v$ のみ含む区間を採用する。
次の図は、例として頂点 $6$ に注目したときに操作するノードを薄い橙色で塗ったものです。集約のために区間を得るときは左側 (fold) 、一点更新をするときは右側 (point) のようにします。どちらも、操作するノードの個数は高々 $\lfloor 2 \log_2 n \rfloor + 1$ です。
ある頂点がデータ構造全体で $O(\log n)$ 回現れ、クエリごとに $O( \log n)$ 個の区間を処理するので、領域木とよく似ています。
問題例
次の問題を考えます。
出典:日本情報オリンピック 2021/2022 春季トレーニング合宿 3 日目 sprinkler 改題
はじめ、 $A_i=1$ である。 $M$ $(2 \leq M)$ が与えられる。 $N$ 頂点の木で次のクエリを合計 $Q$ 個処理せよ。
- $(1,v,d,x)$ :頂点 $v$ から距離 $d$ 以下の頂点 $i$ すべてについて、 $A_i$ を $xA_i$ で置き換える。
- $(2,v)$ :$A_v$ を $M$ で割ったあまりを出力せよ。
素直に処理すると計算量 $O((N+Q) (\log N)^2)$ です。構築は $O(N \log N)$ にできるのでその場合の計算量は $O(N\log N + Q(\log N)^2)$ です。
sprinkler 解答例

heavy light decomposition との融合
参考文献:
↑このブログ投稿はいろいろ書いてあるので、 [*] でこの投稿を参照します。
次のマージ過程を考えます。
- 各辺に頂点を $1$ 個挟んで heavy light decomposition を行い、得られる補助的な木を考える。
- 頂点 $v$ に light edge を表す子が $1$ つ以上あるとき、それらをマージテク $\text{A2}$ でまとめあげ、マージ過程を表す木の根を頂点 $v$ の子にする。
- heavy path は頂点が並んだものであるが、これはマージテク $\text{A}$ でまとめあげる。
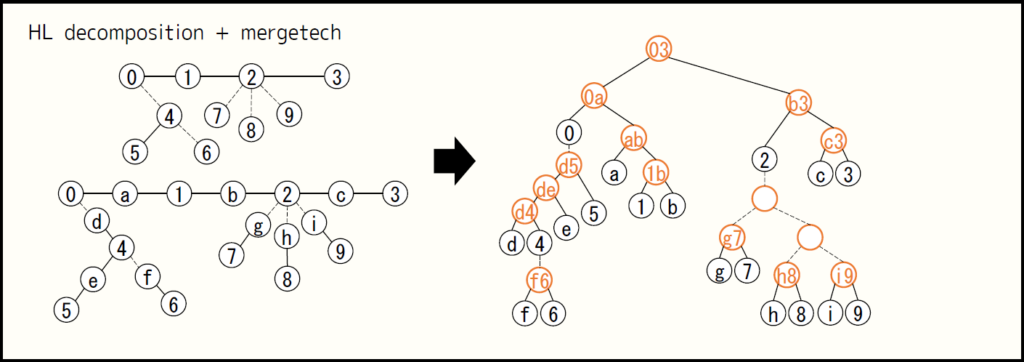
マージ過程に現れる要素には heavy path 上の頂点が抜けて辺が浮いていて、部分木として扱えないものもありますが、 boundary vertex が抜けた cluster としては扱えます。
また、頂点と辺のサイズをそれぞれ $1$ とすると、マージ過程を表す木の高さは高々 $\lfloor \log_2 n \rfloor + 2\lfloor \log_2 (2n) \rfloor + 3\lfloor \log_2 n \rfloor = 6 \lfloor \log_2 n \rfloor +2$ となり、 $O( \log n)$ を保ちます。
マージ過程を表す木が二分木になったので、セグメント木とみなせます。これで、 heavy light decomposition + セグメント木でパスクエリを処理するときの、セグメント木の高さの総和を $O( \log n)$ で抑えることができました。よすぽの日記によると、 $O( \log n)$ に改善しても実行時間であまり効果が見られていないように思えるので、実用上は heavy path ごとに通常のセグメント木を乗せればよいでしょう。
類似
さきほど紹介したのはとりあえず色々できて葉木の二分木にできるようにしたものですが、目的を絞ればもっとシンプル、あるいは定数倍の小さい方法が考えられます。
静的な top tree
cluster のマージ過程を二分木で表します。新しい heavy path (+ light edge $1$ 本)をマージで表すとき、 point cluster と edge cluster が混ざった列をまとめることになり、過程で compress と rake (niuez’s diary などを参考に)が入り混じりますが、位置関係さえ守ればどの順番でマージしても表現できます。そしてこれはマージテク $\text{A}$ です。木の高さは $4\log_2 n+O(1)$ です。
パスクエリ用の HLD
投稿 [*] で紹介されています。
light edge が二分木をなす必要がない場合(トップダウンの探索が不要)を考えます。パスクエリを処理するにはこれで充分です。 light edge は親からのリンクが不要なので、いくつかの heavy path を $1$ つの頂点に直接結びます。マージテク $\text{A}$ を適用すると、 light edge と合わせて木の高さは $5\log_2 n+O(1)$ です。
ここで、マージテク $\text{A}$ の二分木を葉木にするのではなく、各ノードにも単位データを持たせます。すると、マージテク $\text{A}$ の二分木において重み $x$ のノードの深さが $\lfloor\log_2 \frac{n}{x} \rfloor$ となり、全体の木の高さが $2\log_2 n+O(1)$ となります。
重心分解+マージテクとの互換性
この構造を用いて、重心分解とマージテクの融合の機能を再現できます。
- 得られる二分木の各ノードに対応する「部分木の根」が必要ですが、それはマージされる $2$ つの cluster が共有する頂点にします。
- 頂点にデータを乗せる場合は、各頂点から辺を生やした状態から分解すればよいです。
これらに気を付ければ、こちらも disjoint な部分木への分解なので、重心分解と同様の計算ができます。これは top tree に乗るので、木の高さは $4\log_2 n+O(1)$ です。
また、この工夫を用いたうえで cluster 以外を許すと、重心分解+マージテクによる木の高さを $\log_{\frac{3}{2}}n\approx 1.71\log_2n$ にすることができます。その方法は投稿 [*] で紹介されています。
問題例
次の問題を考えます。
出典: noshi91 ブログ
$N$ 頂点の木が与えられます。 $k=0,1, \ldots , N$ について、 $k$ 頂点の独立集合の個数を $\bmod$ $998244353$ で出力してください。
これを DP で解くためには、外部と接続されている頂点の個数が少ない部分木を選んで問題を解く必要がありますが、 cluster はそれを達成します。計算結果のマージは数回の畳み込み(コスト $O((a+b) \log (a+b))$ )ですから、マージテク $\text{A}$ に相当する構造を作らないと、効率的に計算できません。
heavy light decomposition とマージテク $\text{A}$ を融合した構造を用いて、 cluster 単位で計算すると、全体で計算量 $O(N (\log N)^2)$ を達成できます。
(*2) (2022/09/01追記)このときのマージ過程から二分探索木を得ますが、それに相当するものに “biased binary tree” という名前がついているという指摘が codeforces blog comment にあります。 (Samuel W. Bent, Daniel D. Sleator and Robert E. Tarjan. Biased Binary Trees.) に定義があるようです。ただし、少なくとも定義の過程が異なるので、本当にそう呼んでよいのか筆者は知りません。
不具合の連絡は twitter:@NachiaVivias へ