本投稿では、
- JOI の問題 Sprinkler に代表されるように、木の頂点 $v$ からの距離が $d$ 以下の頂点の集合を参照したいとき、木の頂点数を $n$ として $O(n)$ 空間で処理する方法
- BFS Numbering (*1)を用いて等高線クエリを処理するための対象区間を高速に得る方法
- 区間辺の場合の高速化
を説明します。
(*1) BFS Numbering 参考 : JOI 2021/22 春合宿 Day 3 スプリンクラー (Sprinkler) 解説 page 21 (https://www2.ioi-jp.org/camp/2022/2022-sp-tasks/contest3/sprinkler-review.pdf#page=21)
表記
$n$ は木の頂点数です。頂点を任意に $1$ つ選んで根として、根付き木として扱います。頂点に番号をつける場合は $0,1,\ldots ,n-1$ を付け、 $0$ を根とします。
頂点 $v$ の深さを $\text{depth}(v)$ で表します。
BFS Numbering
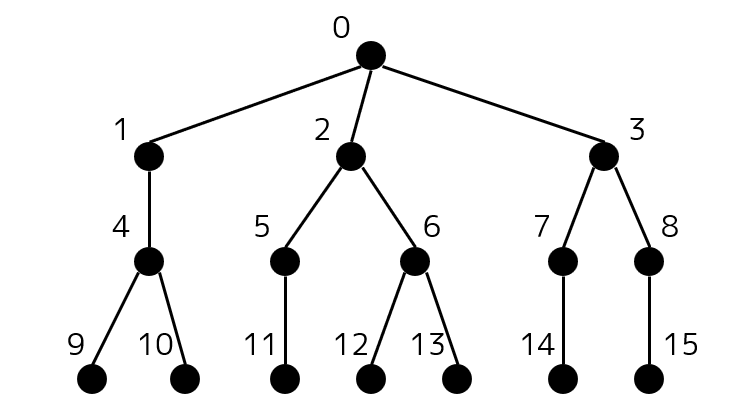
木があるとき、まず深さ優先探索の行き掛け順に頂点を並べます。探索中に子を選ぶ順番は任意とします。 $0\leq d\leq n-1$ について、この頂点列から深さ $d$ の頂点を取り出した部分列をとり、それらを $d$ の昇順に連結したものを $S_{\text{BFS}}$ とします。この頂点列を使うテクニックは BFS Numbering と呼ばれることがあります。
(別の定義) : $S_{\text{BFS}}$ は、次の幅優先探索アルゴリズムで生成される bfs であると定義できます。
// 幅優先探索による S_BFS の生成
vector<int> bfs;
bfs.push_back(0);
for(int i=0; i<n; i++){
int v = bfs[i];
for(int w : children_of(v)){
bfs.push_back(v);
}
}
水平集合
頂点 $v$ と非負整数 $d$ を任意に選んだとき、頂点 $v$ の子孫であって深さが $d$ であるような頂点からなる集合を水平集合と呼ぶことにします。これを $S _ {v,d}$ で表します。空集合でない場合、 $d$ を水平集合の深さということにします。
この水平集合が本投稿の内容全体の軸になります。
以下は水平集合の性質です。
- 任意の水平集合に対して、要素の集合が一致するように $S_{\text{BFS}}$ の連続部分列をとれます。
- 水平集合の個数は $2n-1$ 以下です。頂点数 $2^k-1$ の完全二分木において水平集合は $2^k-k-2$ 個です。
- 水平集合全体はラミナー族をなします。つまり、共通部分をもつどの $2$ つの水平集合も、ある一方が他方を包含します。
下降木
定義
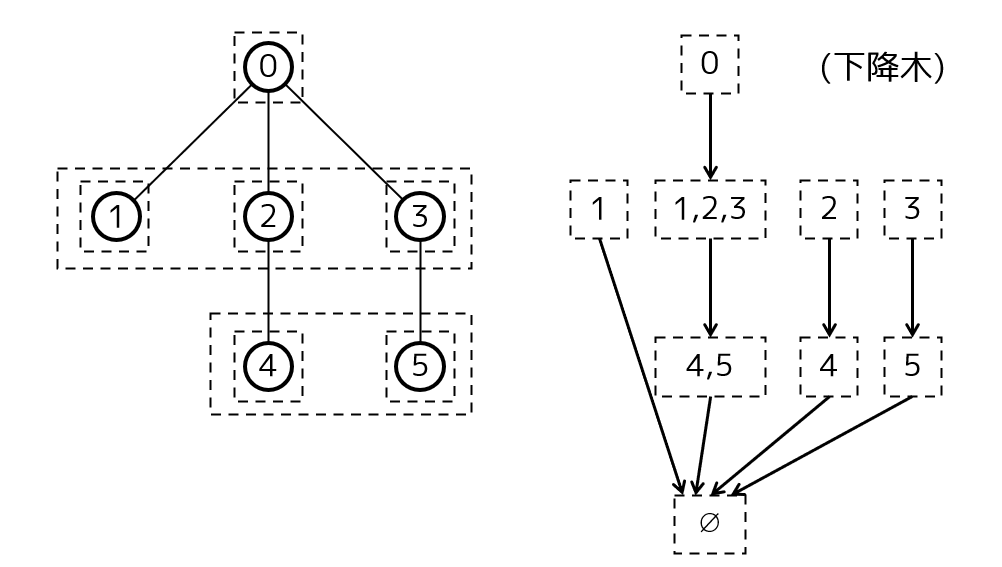
ある空でない水平集合 $S _ {v,d}$ について、 $S _ {v,d}$ の要素の子全体の集合は、 $S _ {v,d+1}$ であるため水平集合です。水平集合に対応する頂点をもち、 $S _ {v,d}$ から $S _ {v,d+1}$ に向けて辺をもつ有向グラフは、すべての辺が空集合 $\varnothing$ に近づく方向を向いている有向木です。これを下降木と呼ぶことにします。下降木における親への遷移を下降遷移と呼ぶことにします。
水平集合の頂点の親からなる集合が水平集合であるとは限らず、例えば下図において $S _ {0,2}=\lbrace 4,5\rbrace$ の頂点の親をちょうど含む集合 $\lbrace 2,3\rbrace$ は水平集合ではありません。ただし、ラミナー性より、 $S _ {v,d}$ が含む頂点の親をすべて含む水平集合のうち最も要素数が小さいものは一意です。それで決まる集合に移る遷移を上昇遷移と呼ぶことにします。
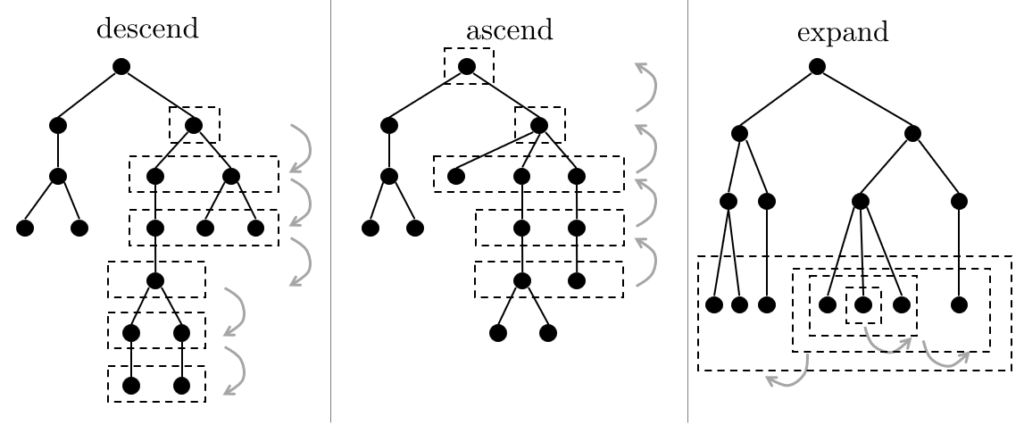
さらに、ラミナー性より、任意の水平集合 $S _ {v,d}$ について、 $S _ {v,d}$ を包含するような $S _ {v,d}$ 以外の水平集合のうち最も小さいものは存在すれば $1$ つに定まります。このような遷移を拡大遷移と呼ぶことにします。ある空でない水平集合 $X$ を $X=S _ {v,d}$ と表せるときの $v$ の深さの最大値を $X$ の基点と言うことにします。 $S _ {v,\text{depth}(v)}=\lbrace v\rbrace$ の基点は $\text{depth}(v)$ です。
$X=S _ {v,d}$ の基点が $\text{depth}(v)$ であるような水平集合は、 $\lbrace v\rbrace$ から始めて基点が $\text{depth}(v)$ である限り下降遷移を続けると、すべて得られます。
以降では、必要に応じて下降,上昇,拡大遷移をそれぞれ $\text{descend}(X)$ , $\text{ascend}(X)$ , $\text{expand}(X)$ と表します。
計算
降下木と各遷移を、 $O(n)$ 時間で計算します。
深さが大きい頂点から順に $v$ に代入し、 $v$ についての計算では $v$ の部分木に含まれる頂点 $w$ についての $S _ {w,d}$ たちで完結する遷移がすべて計算されるようにします。
$S _ {v,d(v)}=\lbrace v\rbrace$ 以外で、 $S _ {v,d}$ で初めて現れる集合の個数は、 $v$ の子の部分木のうち高さが $2$ 番目に大きいものの高さ + $1$ です。その個数を $h$ とおいたとき、新しい水平集合 $S _ {v,d(v)},S _ {v,d(v)+1},\ldots ,S _ {v,d(v)+h}$ について以下の手順で遷移を決定します。
- (1) $\text{descend}(S _ {v,d})=S _ {v,d+1}$ 。 ($d-\text{depth}(v)=0,1,\ldots ,h$)
- (2) $\text{ascend}(S _ {v,d+1})=S _ {v,d}$ 。 ($d-\text{depth}(v)=0,1,\ldots ,h-1$)
- (3) $v$ の子 $w$ について、 $\text{expand}(S _ {w,d})=S _ {v,d}$ 。 ($d-\text{depth}(v)=1,\ldots ,h$ , $S _ {w,d}\neq \varnothing$)
- (4) $v$ の子 $w$ について、 $\text{ascend}(S _ {w,\text{depth}(v)+1})=S _ {v,\text{depth}(v)}$ 。
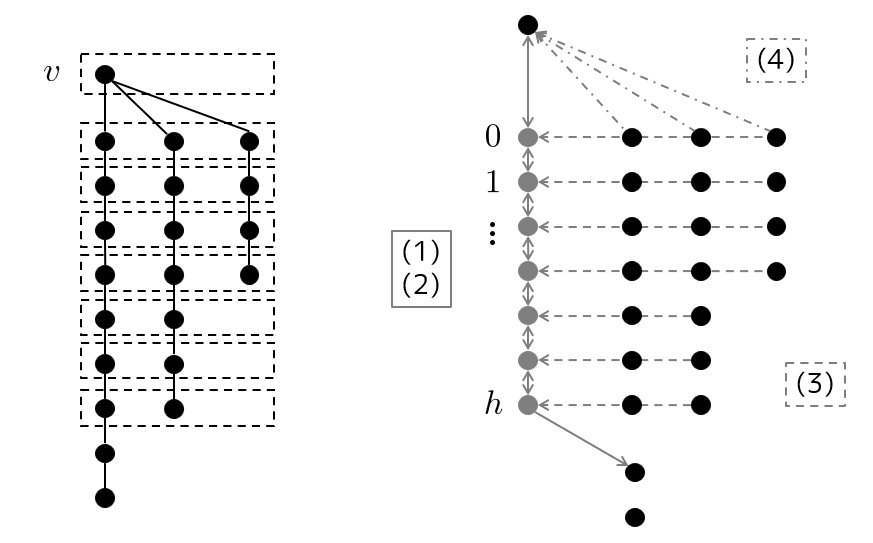
$d=0,1,\ldots$ と変化させるところでは、すでに求まっている下降遷移を用いて対象の水平集合を得られます。手順で決定されなかった遷移先は、計算の都合上では空集合 $\varnothing$ としておけば以降では困りません。
距離が K 以下の頂点の集合
頂点 $v$ からの距離が $K$ 以下の頂点の集合は、非交差な $2K+1$ 個以下の水平集合の併合で表せます。具体的には、 $p^0(v)=v$ とし、 $p^{k}(v)$ の親を $p^{k+1}(v)$ とすれば、次の $2K+1$ 個の集合で表せます。
- $S _ {p^{k}(v),\text{depth}(v)+K-2k}$ ($k=0,1,\ldots ,K$)
- $S _ {p^{k}(v),\text{depth}(v)+K-2k-1}$ ($k=0,1,\ldots ,K-1$)
JOI 2021/22 春合宿 Day 3 スプリンクラー (Sprinkler) 解説 page 19
計算
これらの水平集合は、下降木における $S _ {p^{k}(v),\text{depth}(p^{k}(v))}$ ($=\lbrace p^{k}(v) \rbrace$) の level ancestor として計算することができます。 level ancestor problem は定数時間で解けるので $O(K)$ 時間ですべての集合が得られます。
一方で、上で計算した遷移を活用すれば、次の方法で $O(K)$ 時間ですべての集合が深さの降順に求まります。
- $X=\lbrace v\rbrace$ , $d=0$ から始める。
- $k=K,K-1,K-2,\ldots ,-K$ について以下を実行する。
- $X$ の基点が $\text{depth}(v)-\lfloor (K-k)/2 \rfloor$ 以上となる限り、 $X$ を拡大遷移させ続ける。
- $X$ が空集合にならず、かつ $d\leq k$ となる限り、 $X$ を下降遷移させて $d$ に $1$ を加算することを続ける。
- $d=k$ の場合、 $X$ を採用し、 $X$ を $1$ 回上昇遷移させて $d$ に $1$ を減算する。
- $X$ が空集合であるとき、すでにすべての集合が求まっているので手順を終了する。
手順中、 $d$ は $X$ の深さから $\text{depth}(v)$ を引いた値を表します。また、 $v$ の $\lfloor (K-k)/2 \rfloor$ 個親を $p^{k^{\prime}}(v)$ とすると、各ループの 1. 実行後は $X=S _ {p^{k^{\prime}}(v),d+\text{depth}(v)}$ を満たします。
計算量
繰り返しがあり、計算量が非自明です。
アルゴリズム全体の動作は次の $2$ 段階に分かれます。
- (A) 下降遷移と拡大遷移を繰り返す。
- (B) 上昇遷移と拡大遷移を繰り返す。
(A) では、 $k$ のループ $1$ 回ごとに拡大遷移は高々 $1$ 回であること、下降遷移の回数は $d\leq k$ で抑えられていることから計算量が抑えられます。前者は条件 $X=S _ {p^{k^{\prime}}(v),d+\text{depth}(v)}$ から示せます。
(B) では、拡大遷移によって基点の値は減少し、また上昇遷移によって基点の値が増加しないことから遷移回数が抑えられます。
以上より、遷移回数は $O(K)$ であり、計算量も $O(K)$ になります。
例題
$n$ 頂点の木と $2$ 以上の整数 $L$ 、 $0$ 以上 $L$ 未満の整数 $A _ 0,A _ 1,\ldots ,A _ {n-1}$ が与えられます。以下のクエリを合計 $Q$ 個処理してください。
- (A) $x$ , $d$ , $w$ が与えられるので、頂点 $x$ からの距離が $d$ 以下であるような頂点 $y$ それぞれについて、 $A _ y$ の値を($wA _ y$ を $L$ で割ったあまり)で更新してください。ただし、 $d\leq D$ を満たす $D$ が決まっているとします。
- (B) $x$ が与えられるので、 $A _ x$ の値を答えてください。
おなじみ Sprinkler です。
水平集合ごとに寄与を管理します。 (A) では、分割後の水平集合それぞれの寄与に $x$ を掛けます。計算量は $O(D)$ です。
(B) では、頂点 $x$ を含む水平集合を拡大遷移で列挙しながら、基点が $\text{depth}(x)-D$ 以上である範囲について寄与を集計します。計算量は $O(D)$ です。
よって、全体の計算量は $O(N+QD)$ であり、また空間計算量は $O(N)$ です。
実装例
AtCoder の Sprinkler のジャッジに提出してあります。

等高線集約クエリ
次の問題は、木上の等高線集約クエリ – suisen のブログ で言及された問題です。
クエリとして組 $(v,d)$ が与えられます。 BFS Numbering による頂点列 $S _ {\text{BFS}}$ の連続部分列を $0$ 個以上取り出し、その和集合が、頂点 $v$ との最短距離が $d$ であるような頂点の集合に一致するようにしてください。
suisen のブログでも言及があるように、 $S _ {\text{BFS}}$ の取り方にかかわらず、必要な集合を $O(\sqrt{n})$ 個の連続部分列で表すことができます。 $v$ からの最短距離が $d$ である頂点をとって $w$ とし、 $\text{LCA}(v,w)$ で分類すればそれぞれは高々 $2$ つの連続部分列で表せます。 $vw$ 間のパスのうち $v$ から根のパスに含まれない部分に注目すると、 $\text{LCA}(v,w)$ で分類するごとに新しい頂点が少なくとも $0,1,2,\ldots$ 個必要になるため、全体で $n$ 頂点であるためには $\text{LCA}(v,w)$ の種類数は $O(\sqrt{n})$ にならなければなりません。
事前処理として、答えが変わらない限り $v$ を根に近づけます。具体的には、「 $v$ の祖先 $w$ であって、 $w$ の部分木の高さが $d-\text{depth}(v)+\text{depth}(w)-2$ 以上となるもののうち最も根から遠いもの」を求めることになります(下図参照)。条件を満たす頂点が存在しない場合は、頂点 $v$ との最短距離が $d$ であるような頂点が存在しません。
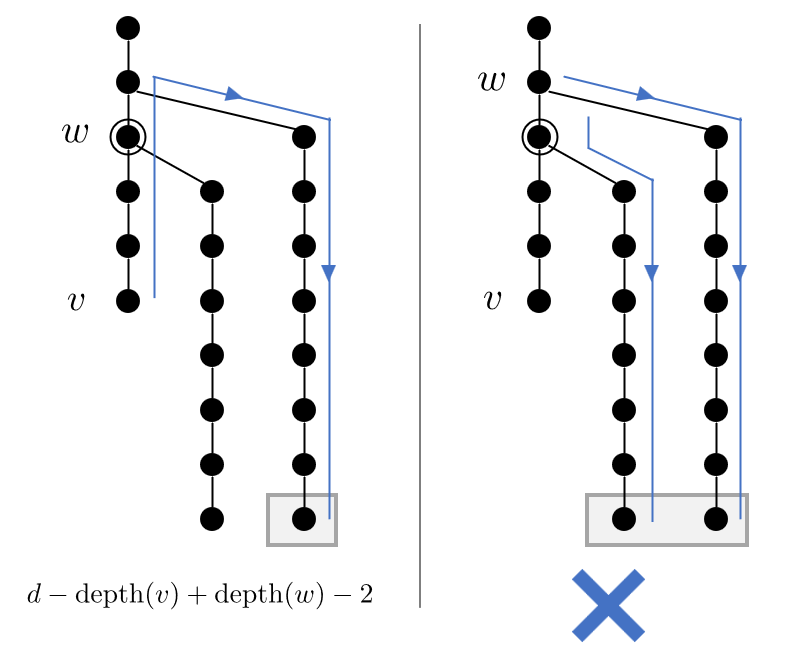
$v$ からの最短距離が $d$ である頂点 $w$ のうち、 LCA が $g$ であるものの集合を考えます。 $g=v$ のときこれは $S _ {v,\text{depth}(v)+d}$ です。 $g=w$ のときは $\lbrace w\rbrace$ です。
$g\neq v$ かつ $g\neq w$ のときは、 $g$ から $v$ に近づく方向に $1$ つだけ進んだ頂点を $f$ とすると、水平集合の差 $S _ {g,2\text{depth}(g)+d-\text{depth}(v)}\setminus S _ {f,2\text{depth}(g)+d-\text{depth}(v)}$ で表せます。 $d _ q=d-\text{depth}(v)$ とおき、この集合を $Q(f,d _ q)$ と表します。これが空集合でない場合、 $S _ {g,2\text{depth}(g)+d _ q}$ の基点は $\text{depth}(g)$ です。よって、 $g\neq v$ かつ $g\neq w$ の範囲で採用される集合を次で説明できます:
- $v$ の祖先 $f$ について、 $f$ の親を $g$ として $S _ {g,2\text{depth}(g)+d _ q}$ の基点が $\text{depth}(g)$ である場合、 $Q(f,d _ q)$ を採用する。
ただし、 $S _ {f,2\text{depth}(g)+d _ q}=\varnothing$ である可能性は、事前処理によって排除されています。(つまり、もし $S _ {f,2\text{depth}(g)+d _ q}=\varnothing$ が成り立つなら $v$ を $v$ の親に置き換えても答えが変化しません。)
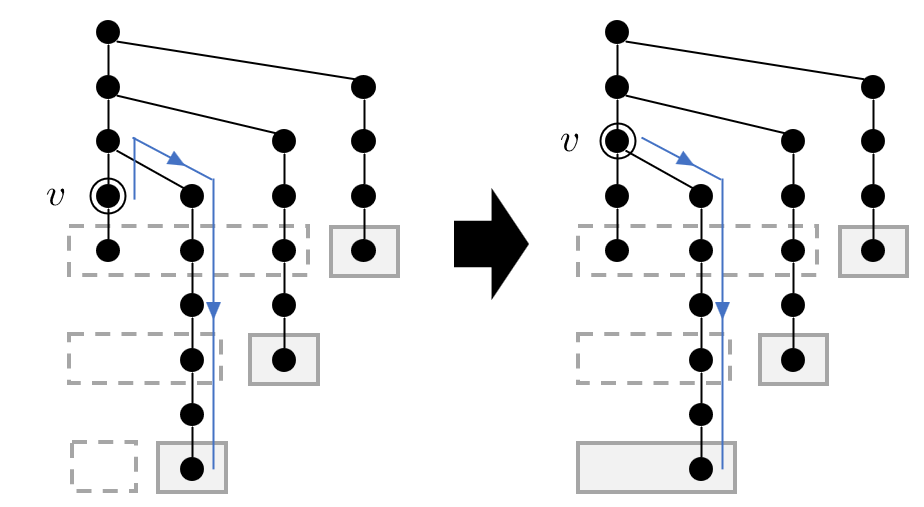
任意の空でない水平集合 $X$ について、 $\text{expand}(X)\setminus X$ が採用されうるような $d _ q$ の値は高々 $1$ 通りです。同じ $d _ q$ に属する水平集合 $X$ どうしで $f$ が根に近づく方向の遷移をあらかじめ計算しておいたのち、 $Q(f,d _ q)$ が採用される $f$ のうち深さが最大のものが求まれば残りはすべて連鎖的に得られます。
計算
適切に値 $\delta (w)$ をとれば、事前処理の計算内容は「 $v$ の祖先 $w$ であって、 $d _ q\geq\delta (w)$ となるもののうち最も根から遠いもの」と表せます。このとき、 $w$ を根に近けると $\delta (w)$ の値は単調増加します。よって、事前処理に必要な計算は、 heavy-light decomposition を利用した探索によって存在判定も含めて $O(\log n)$ 時間で計算できます。
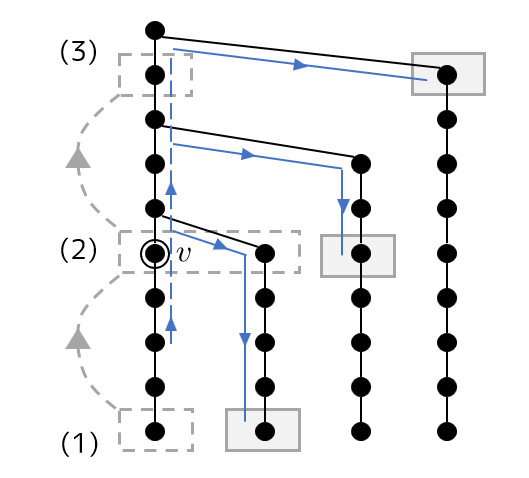
元の木を深さ優先探索しながら、 $\lbrace x\rbrace$ から下降遷移で得られる水平集合 $X$ のうち $\text{expand}(X)$ の基点が $\text{depth}(x)-1$ であるものについて $\text{expand}(X)\setminus X$ を処理します。これにより、走査時点において、各 $d _ q$ について $Q(f,d _ q)$ であって $f$ が $x$ の祖先であるもののうち $f$ が最も $x$ に近いもの (これを $F(x,d _ q)$ とおきます ) を取得でき、これにより $f$ を順に根に近づけてゆくための遷移も計算できます。さらに、 $F(x,d _ q)$ の情報が、深さ優先探索の行きがけ順でランレングス圧縮したものとして明示的に取得できます。(下図参照)
$g=v$ について、 $S _ {v,\text{depth}(v)+d}$ は下降木の level ancestor から計算できます。 $g=w$ について、 $v$ の $d$ 段階親 $w$ が存在すれば $\lbrace w\rbrace$ を加えます。
$g\neq v$ かつ $g\neq w$ について、最初の $Q(f,d _ q)$ を $F(x,d _ q)$ のランレングス圧縮から二分探索で検索して取得し、残りの $Q(f,d _ q)$ を遷移から次々に取得します。
以上より、 $O(n)$ 時間の前計算のもと、この方法で採用される $S _ {\text{BFS}}$ の連続部分列の個数を $M$ として $O(\log n+M)$ 時間でクエリの答えを得られます。なお、 $M$ の値は $O(\sqrt{n})$ になります。
区間辺
いわゆる区間辺というテクニックにおいては、等高線集約のクエリ当たりの計算量が抑えられます。
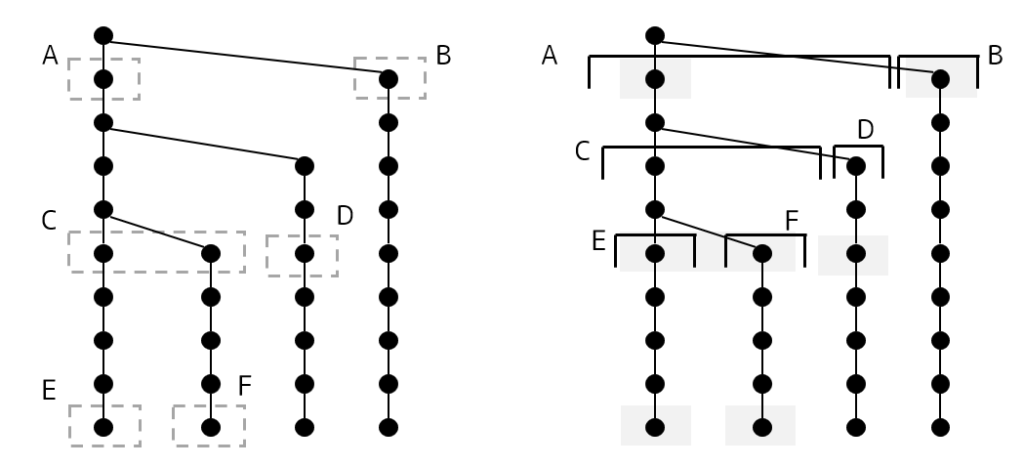
水平集合に対応するノードは、拡大遷移に従えば得られます。$Q(f,d _ q)$ に対応するノードを作るには、水平集合の列の両側から累積和を作り、それぞれから $1$ 個ずつを参照するノードを追加すればよいです(下図参照)。
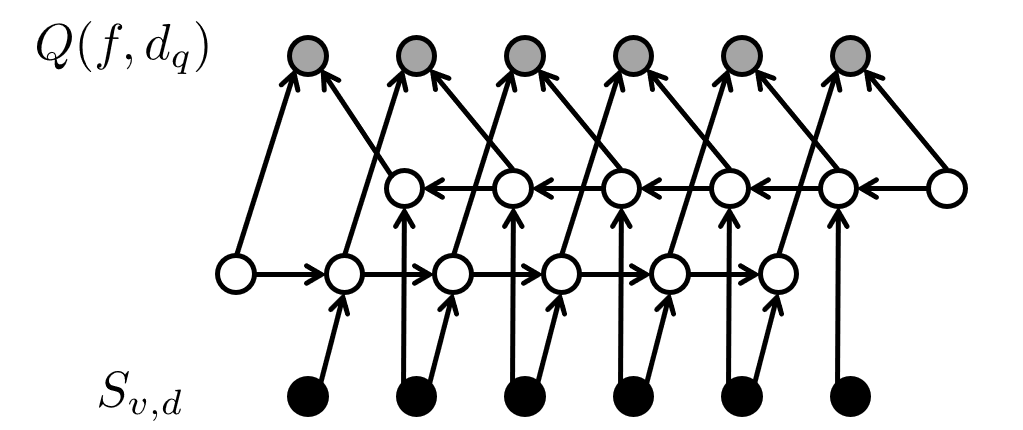
$Q(f,d _ q)$ の連鎖に従ってノードを追加し、それらと水平集合のノードを参照することで、求める集合を集約したノードが得られます。前計算は $O(n)$ 時間で、クエリ当たりの追加ノード・辺の個数は $O(1)$ 、計算量は $O(\log n)$ です。
例題
$n$ 頂点の木 $T$ が与えられます。また、頂点番号を共有する $n$ 頂点のグラフ $G$ があり、はじめは $G$ の任意の $2$ 頂点間に重み $C$ の辺があります。さらに、 $k=0,1,\ldots ,K-1$ について、以下の条件で $G$ に辺を追加します。
- $v _ k$ , $w _ k$ , $d _ k$ , $c _ k$ が与えられるので、 $T$ 上での $w _ k$ からの距離が $d _ k$ である頂点 $x$ すべてについて、 $G$ において $v _ k$ , $x$ の間に重み $c _ k$ の辺を追加する。
こうしてできたグラフ $G$ において単一始点最短経路を計算してください。
最短経路問題は区間辺が有効な典型問題です。この問題は $O(n+K)$ 頂点 $O(n+K)$ 辺の重み付きグラフの単一始点最短経路問題に変換できます。
実装例
ランダムテストで使用したプログラムを公開します。

おわり