splay tree をソラで書く！！！

(2023/02/05) 実はここに書いた方法はとにかく覚えにくいので、今度新しく書きます。考察不足でしたのでおわび申し上げます。

動機の例

自作ライブラリで Library Checker の問題^[1]を解きたい
link/cut tree を実装したい
splay tree の面白い機能を思いついたときに実装したい
平衡二分探索木や動的木が JOI に出る(?)^[2] ^{[3] ネタバレ注意}
PCK に出る(?)^{[4] ネタバレ注意}

目標

平衡二分探索木の一種である (bottom-up の) splay tree の C++ 言語による実装例を示す
splay tree を覚えやすい・一発で書きやすい方法で実装し、注意点をまとめる
注意点はできるだけ多くの点を挙げ、実装の方針が同じ splay tree が正しく動作しなかったときのチェックリストになるようにする
この実装を用いて Library Checker の Dynamic Sequence Range Affine Range Sum^[1] （以下、 verifier と呼ぶ）に正解する
一度ソラで書く

導入

機能

verifier に正解するために必要な機能を持ちます。詳しく/正確には verifier を参照してください。

insert_at(p,x) ：位置 $p$ に要素 $x$ を挿入。
erase_at(p) ：要素 $p$ を削除。
reverse(l,r) ：区間 $[l,r)$ を反転。
apply(l,r,f) ：区間 $[l,r)$ に $f$ を作用。
prod(l,r) ：区間 $[l,r)$ を集約した値を取得。

以上の操作の時間計算量はそれぞれ均し $O(\log n)$ です。

短くいうと、挿入、削除、区間 reverse ができる遅延セグメント木です。

原理

この記事では、 splay tree の原理にあたる部分はすでに知っているものとします。次のような別の記事を参考にしてください。

[5] Wikipedia
[6] JOI のある問題の解説スライド (115ページから197ページが splay tree の解説）
[7] yaketake08 さんによるビジュアライザ

splay tree の特徴

splay tree を発表する論文^[8]は Daniel Sleator さんと Robert Tarjan さんによって 1984 年に書かれ、1985年に出版されました。

均し（償却、 $\text{amortized}$ ）計算量

頂点数 $n$ の splay tree で行う操作 $1$ 回ごとに時間計算量が $O(\log n)$ となるわけではありません。

splay tree の各頂点 $v$ について部分木の頂点数を $w(v)$ とし、 $\Phi=\sum_v \log w(v)$ とおきます。すると、 splay 操作による $\Phi$ の増加量と時間計算量の和が $O(\log n)$ となります。 splay 以外の操作も同様に、 $\Phi$ の増加量と時間計算量の和が $O(\log n)$ となるように設計します。

一方、他の二分探索木の例である AVL tree や red-black tree は、頂点数 $n$ の二分木の高さは $O(\log n)$ となり、検索 $1$ 回ごとの計算量が $O(\log n)$ で抑えられます。^[9] ^[10] また、乱択を用いる二分探索木 treap だと検索の計算量は期待 $O(\log n)$ 、単純な挿入で構築する二分探索木だと検索の計算量は平均 $O(\log n)$ となります。^[11]

構造が柔軟

Splay Tree は構造の姿勢に直接の制約がありません。重要な例として、均し $O(\log n)$ 時間で、管理する列の任意の区間について、それを集約するノードを得ることができます。これを用いて均し $O(\log n)$ 時間の reverse 操作を実現し、さらに他の区間クエリの処理を簡潔に実装します。

動的木への応用

splay tree を改造することで link/cut tree を実装できます。ちなみに、 link/cut tree を発表する論文^[12] は同じ 2 人によって splay tree よりも早く、1982年に書かれました。

実装・解説

基本構造(の基本）

実装の方針

頂点の情報を struct Node にまとめます。
現時点の頂点の集合を std::vector<std::unique_ptr<Node>> の型で管理します。
その他、頂点を参照する場合はポインタ型 Node* を使います。
頂点がないことを表す仮想頂点 NIL を用意し、 Splay Tree のコンストラクタで初期化します。
根を R として参照します。

実装例

展開

#include <vector>
#include <memory>
using namespace std;
struct SplayTreeByIdx{
    struct Node{ // 暫定的
        Node *l=0, *r=0, *p=0;
    };
    using pNode = unique_ptr<Node>;
    pNode pNIL;
    Node *NIL = nullptr;
    vector<pNode> A;
    Node *R;
    SplayTreeByIdx(){
        if(!pNIL){
            pNIL = make_unique<Node>();
            NIL = pNIL.get();
            NIL->l = NIL->r = NIL->p = NIL;
            R = NIL;
        }
    }
    // ...
};

基本構造（クエリ依存）

実装の方針

原則 AtCoder Library の lazy_segtree と同じ形式で定義します。ただし、 reverse 時の集約値の変化を考慮しなければなりません（一般的には逆順で集約したものも持っておいて reverse 時にスワップすればよい）。
reverse も遅延伝播します。
頂点の削除時の配列 A の更新のため、頂点に、対応する A の添え字を結びつけます。

実装例

展開

const unsigned int MOD = 998244353;

// ほぼ atcoder::lazy_segtree と同じ
struct S{ unsigned long long x,z; };
static S op(S l, S r){ return { (l.x + r.x) % MOD, l.z + r.z }; }
static S e(){ return {0,0}; }
static void reverse_prod(S& x){  } // 反転時に prod を更新する
struct F{ unsigned long long a,b; };
static S mapping(F f, S x){ return { (x.x * f.a + x.z * f.b) % MOD, x.z }; }
static F composition(F f, F x){ return { f.a * x.a % MOD, (f.a * x.b + f.b) % MOD }; }
static F id(){ return {1,0}; }

struct Node{
    Node *l = 0, *r = 0, *p = 0;
    S a = e(); // 頂点が持つ値
    S prod = e(); // 集約（ rev==1 のときでも reverse_prod 作用済み）
    F f = id(); // 遅延（a,prod には作用済み）
    int i = -1; // 配列の index
    int z = 0; // 頂点の重み ( NIL なら 0 、普通の頂点は 1 ）
    int sumz = 0; // 部分木の重み
    int rev = 0; // 反転の遅延
};

伝播・集約

実装の方針

指定したノードで伝播 or 集約をする関数を用意します。

実装の注意点

実装例では、集約（ prepareUp ）は、要件としてそのノードで伝播が済んでいることを要求します。

実装例

展開

// in struct SplayTree
// 伝播
void prepareDown(Node* c){
    if(c->l != NIL){
        // a,prod への作用を忘れずに
        c->l->a = mapping(c->f, c->l->a);
        c->l->prod = mapping(c->f, c->l->prod);
        c->l->f = composition(c->f, c->l->f);
    }
    if(c->r != NIL){
        // a,prod への作用を忘れずに
        c->r->a = mapping(c->f, c->r->a);
        c->r->prod = mapping(c->f, c->r->prod);
        c->r->f = composition(c->f, c->r->f);
    }
    if(c->rev){
        swap(c->l, c->r);
        if(c->l != NIL){
            c->l->rev ^= 1; // 伝播
            reverse_prod(c->l->prod);
        }
        if(c->r != NIL){
            c->r->rev ^= 1; // 伝播
            reverse_prod(c->r->prod);
        }
        c->rev = 0;
    }
    c->f = id(); // 伝播済み
}

// 集約
void prepareUp(Node* c){
    c->sumz = c->l->sumz + c->r->sumz + 1; // 部分木の重み
    c->prod = op(op(c->l->prod,c->a),c->r->prod); // 集約　c は伝播済み
}

回転, splay

実装の方針

伝播・集約を splay 関数内で行います。伝播・集約のタイミング、及び計算量の定数倍についてはながたかなさんの投稿^[13] で非常に詳しく解説されていますが、反転の伝播が必要なためトップダウンフェーズに伝播が必要であることに注意してください。
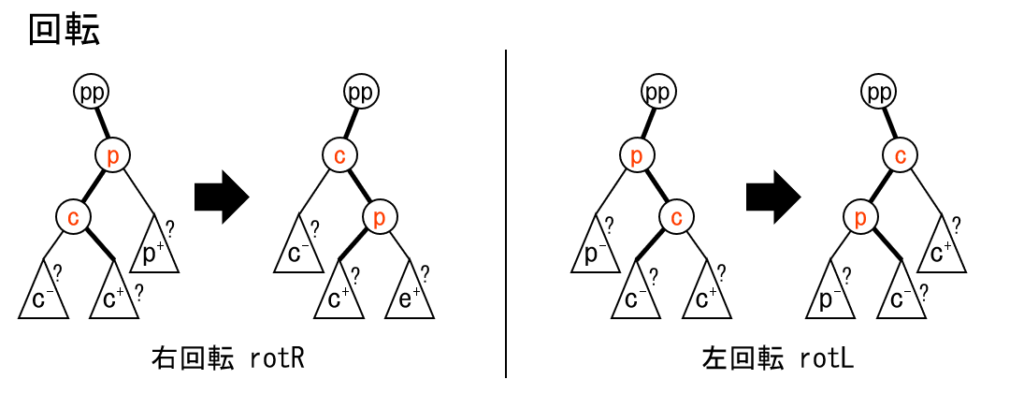
rotL(c) , rotR(c) ：頂点 $c$ の親を軸に左/右回転します。回転前に $c$ と $c$ の親である頂点の遅延伝播/集約は関数外で必ず行います。
splay(c) ：頂点 $c$ を根に移動します。 splay 関数内で必要な伝播を行い、頂点 $c$ の集約値をすぐに得られるようにします。

実装の注意点

伝播は親から順、集約は子から順に行う必要があることに注意してください。
splay で、対象の頂点がすでに根であった場合の伝播・集約に注意してください。
splay 関数内で行う伝播は、実は不要かもしれません。なぜなら、設計によっては、 splay するノードを参照するまでにその祖先はすでに伝播が済んでいる保証があるからです。
例えば c->l->a への代入の前に、子（ c->l ）が NIL である可能性を必ず除きます。 NIL の改変は許されません。

図解・実装例

展開

// in struct SplayTree

// （便利）
// p の親が、子として p を参照するので、それを書き換えられるようにする
// 根の場合に拡張して R の参照を返す。
Node*& parentchild(Node* p){
    if(p->p == NIL) return R;
    if(p->p->l == p) return p->p->l;
    else return p->p->r;
}

// 左回転
void rotL(Node* c){
    Node* p = c->p;
    parentchild(p) = c;
    c->p = p->p;
    p->p = c;
    if(c->l != NIL) c->l->p = p; // 子が NIL かもしれない
    p->r = c->l;
    c->l = p;
}

// 右回転
void rotR(Node* c){
    Node* p = c->p;
    parentchild(p) = c;
    c->p = p->p;
    p->p = c;
    if(c->r != NIL) c->r->p = p; // 子が NIL かもしれない
    p->l = c->r;
    c->r = p;
}

// splay 後、 c は伝播済み
void splay(Node* c){
    prepareDown(c); // ループが回らない時のために
    while(c->p != NIL){
        Node* p = c->p;
        Node* pp = p->p;
        // 伝播は親から
        if(pp != NIL) prepareDown(pp);
        if(p != NIL) prepareDown(p);
        prepareDown(c);
        if(p->l == c){
            if(pp == NIL){ rotR(c); }
            else if(pp->l == p){ rotR(p); rotR(c); }
            else if(pp->r == p){ rotR(c); rotL(c); }
        }
        else{
            if(pp == NIL){ rotL(c); }
            else if(pp->r == p){ rotL(p); rotL(c); }
            else if(pp->l == p){ rotL(c); rotR(c); }
        }
        // 集約は子から
        if(pp != NIL) prepareUp(pp);
        if(p != NIL) prepareUp(p);
        prepareUp(c);
    }
    prepareUp(c); // ループが回らない時のために
}

kth_element, insert, erase

実装の方針

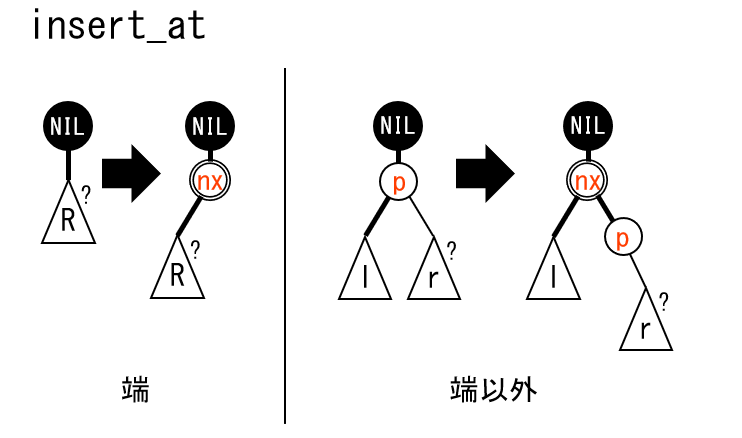
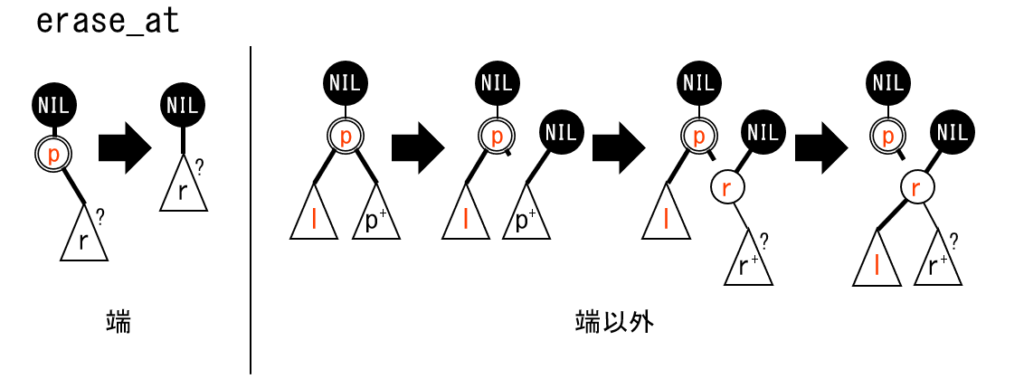
kth_element(k) ：左から $k$ 番目 (0-based) のノードで splay します。
insert(k,x) ：左から $k-1$ 番目 (0-based) のノードのすぐ右に値 $x$ を持つノードを挿入します。 $k=0$ のときは最も左に挿入します。
erase(k) ：左から $k$ 番目 (0-based) のノードを削除します。
$k$ 番目のノードを発見には、 Node::sumz の値（部分木のノード数）を用います。
挿入/削除は、 split / merge を関数内で行うことで、 for や while を使わずに実装します。

実装の注意点

top-down の探索では、ノードに訪れるたびにそのノードで伝播するとよいです。（ reverse によって子の左右が入れ替わっている場合を解消するためなど）
top-down が終わったら、そのノードで splay をしなければなりません。 splay 木とはそういうものです。
端の参照、端への挿入、端のノードの削除、根しかない場合、ノード数 $0$ の場合に注意してください。
端の処理は片側よりも両側について書くほうが、一般の場合の NIL チェックが少なく、バグの予防になります。
erase 時の配列 $A$ の添え字と頂点の対応に注意してください。
insert で追加する頂点のインスタンスの生成では、 NIL をコピーすると楽です。

図解・実装例

展開

// in struct SplayTree
Node* kth_element(int k){
    Node* c = R;
    while(true){
        prepareDown(c);
        if(c->l->sumz == k) break;
        if(c->l->sumz > k){ c = c->l; continue; }
        k -= c->l->sumz + 1;
        c = c->r;
    }
    prepareDown(c);
    splay(c);
    return c;
}

void insert_at(int k, S x){
    pNode pnx = make_unique<Node>(*NIL);
    Node* nx = pnx.get();
    nx->z = nx->sumz = 1;
    nx->i = A.size();
    nx->a = nx->prod = x;
    A.emplace_back(move(pnx));
    if(k == 0){  // 左端
        nx->r = R;
        if(R != NIL) R->p = nx; // 元々 0 頂点かもしれない
        R = nx;
        prepareUp(nx); // 挿入したら集約
        return;
    }
    if(k == R->sumz){ // 右端（左端と同様）
        nx->l = R;
        if(R != NIL) R->p = nx;
        R = nx;
        prepareUp(nx);
        return;
    }
    auto p = kth_element(k);
    nx->l = p->l;
    nx->r = p;
    R = nx;
    p->l->p = nx;
    p->p = nx;
    p->l = NIL;
    prepareUp(p);  // split/merge の影響
    prepareUp(nx); //
}

void erase_at(int k){
    auto p = kth_element(k);
    if(k == 0){ // 左端
        R = p->r;
        if(R != NIL) R->p = NIL; // 0 頂点になるかもしれない
    }
    else if(k == R->sumz-1){ // 右端
        R = p->l;
        if(R != NIL) R->p = NIL;
    }
    else{
        auto l = p->l;
        auto r = p->r;
        r->p = NIL;   // split
        R = r;        //
        kth_element(0);
        r = R;        // merge
        r->l = l;     //
        l->p = r;     //
        prepareUp(r); // split/merge の影響
    }
    swap(p->i,A.back()->i); // index が更新されるよ
    swap(A[p->i],A[A.back()->i]); // 後ろに移動して
    A.pop_back(); // 削除
}

between

実装の方針

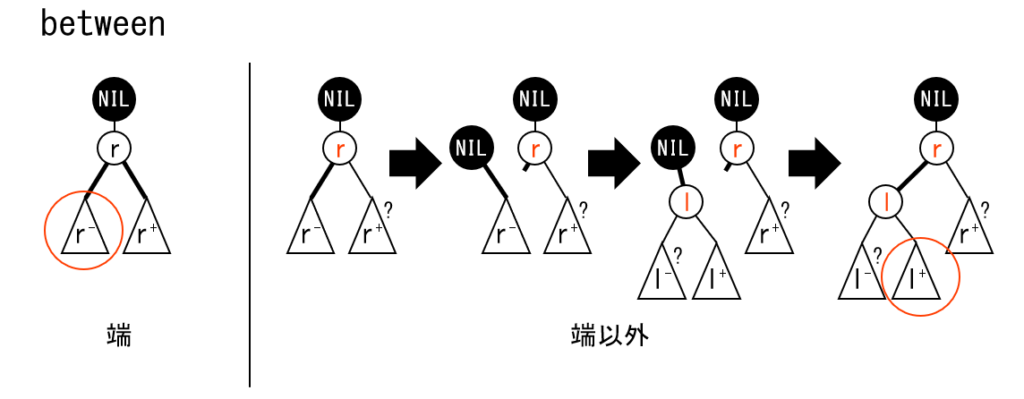
区間クエリを処理するために、区間を集約したノードを取得します。空でない区間については必ず取得できます。
区間が全域でも端でもない場合は split / merge を行います。

実装の注意点

区間が端にある、または全域である場合に注意してください。
split/merge 前後の伝播/集約に注意してください。

図解・実装例

展開

// in struct SplayTree
Node* between(int l, int r){
    if(l == 0 && r == R->sumz) return R; // 全域
    if(l == 0) return kth_element(r)->l; // 左端
    if(r == R->sumz) return kth_element(l-1)->r; // 右端
    auto rp = kth_element(r);
    auto lp = rp->l;
    R = lp;      // split
    lp->p = NIL; //
    lp = kth_element(l-1);
    R = rp;      // merge
    rp->l = lp;  //
    lp->p = rp;  //
    prepareUp(rp); // split/merge の影響
    return lp->r;
}

reverse,apply, prod

実装の方針

reverse、applyは between で取得したノードに作用すればよいです。
prod は between で取得したノードの集約値を返せばよいです。

実装の注意点

ノードに reverse や apply を作用させた直後は、そのノードの伝播が済んだ状態ではないため、 splay や prepareUp の要件を満たさない可能性があります。必要に応じて伝播しましょう。実装例では不要です。
ノードに reverse や apply を作用させた直後は、祖先の集約ができていません。忘れずに、その頂点で splay します。

実装例

展開

// in struct SplayTree
void reverse(int l, int r){
    auto c = between(l,r);
    c->rev ^= 1;
    reverse_prod(c->prod);
    splay(c);
}

void apply(int l, int r, F f){
    auto c = between(l,r);
    c->a = mapping(f,c->a);
    c->prod = mapping(f,c->prod);
    c->f = composition(f,c->f);
    splay(c);
}

S prod(int l, int r){
    return between(l,r)->prod;
}

ゴール

最後に、 verifier の形式に合わせて入出力のコードを書きます。

実装例

}; // end of struct SplayTreeByIdx

#include <iostream>
#include <vector>
#include <memory>
using namespace std;
using i32 = int32_t;
using u32 = uint32_t;
using i64 = int64_t;
using u64 = uint64_t;
#define rep(i,n) for(int i=0; i<(n); i++)

int main(){
  int N,Q; cin >> N >> Q;
  vector<u32> A(N);
  rep(i,N) cin >> A[i];
  SplayTreeByIdx G;
  rep(i,N) G.insert_at(i,{A[i],1});
  rep(i,Q){
    int t; cin >> t;
    if(t == 0){
      int k; u32 x; cin >> k >> x;
      G.insert_at(k,{x,1});
    }
    if(t == 1){
      int k; cin >> k;
      G.erase_at(k);
    }
    if(t == 2){
      int l,r; cin >> l >> r;
      G.reverse(l,r);
    }
    if(t == 3){
      int l,r; u32 b,c; cin >> l >> r >> b >> c;
      G.apply(l,r,{b,c});
    }
    if(t == 4){
      int l,r; cin >> l >> r;
      u64 ans = G.prod(l,r).x;
      cout << ans << "\n";
    }
  }
  return 0;
}

struct ios_do_not_sync{
  ios_do_not_sync(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
  }
} ios_do_not_sync_instance;

以上の実装で、 verifier に正解できます。

実装例をつなげて提出したもの（2113 ms）： https://judge.yosupo.jp/submission/58218

注意点のまとめ

実装の注意点

頂点の子を参照する前に、その頂点で伝播！
頂点の子を参照・編集する前に、 NIL チェック！ NIL の改変は許されません。
根でない頂点（特に between で得られるもの）を編集したら、その頂点で splay！
split/merge 後に集約！
ひたすらにバグ予防！

実際にやってみた

TAKE $1$

$120$ 分で AC が出ず、断念
between で得た頂点を splay するのを忘れるミスがあったので、注意点に追記

TAKE $2$

$46$ 分 $52$ 秒で AC （https://judge.yosupo.jp/submission/58054）
回転を間違えてタイムロス

TAKE $3$

TAKE $2$ の次の日
AtCoder のコードテストでコーディング
$38$ 分 $22$ 秒で AC （https://judge.yosupo.jp/submission/58204）
ウィンドウのキャプチャを投稿しました（https://youtu.be/vKVlWt3mamQ）
一発ではできていない

補足

キーを用いて二分探索木として使いたい

部分木のサイズの代わりにキーを持ちます。
kth_element を改造し、 lower_bound または upper_bound にします。
それ以降の関数で kth_element を使っていた部分を適切に置換します。また、 index を表す引数などは適宜キーで置き換えます。

定数倍高速化の例

split/merge を用いた部分をループ構文を使って書き換える
この実装例では splay する頂点の祖先は伝播済みなので、 splay 中の伝播を省く
回転または splay 時のアルゴリズムを工夫する^[13]
各ノードに伝播済みのフラグを用意し、余分な伝播の実行を防ぐ
同じポインタを参照する部分をキャッシュする
verifier では reverse_prod が不要なので、除く
std::unique_ptr を用いたメモリ管理を除く（当然メモリリークが起こるが、競プロにおいては有用）

などが考えられます。

link/cut tree をソラで書く！！？

狂気実際にやってはいないので方針と少しの注意点だけです。

実装の方針

dashed edge で結ばれた親へのポインタ pp を、 Node 構造体のメンバ変数に追加します。
expose 関数を書きます。
evert （根を変更）関数を書きます。 reverse があるので簡単です。
列としての index でのアクセスより、あらかじめ頂点に振った番号でアクセスするほうが便利と思います。よって、 kth_element 、 insert_at 、 erase_at は不要である場合が多いでしょう。
lca 関数を書きます。
meet は根を変えて lca を使うと得られます。
jump （ xy パス上で x から距離 k の頂点）は splay tree の kth_element に対応します。

実装の注意点

splay 時に祖先が伝播済みである保証はなくなると考えられます。よって、 splay 関数内でも必ず伝播をします。
expose の手順は（「各 splay tree で splay」→「solid edge で結ぶ」→「splay」）を守ります。

参考サイト一覧

私は深く感謝しております。

[1] 今回取り組んだ課題： Library Checker の Dynamic Sequence Range Affine Range Sum
[2] 日本情報オリンピックのとある問題
[3] 日本情報オリンピックのとある問題
[4] パソコン甲子園プログラミング部門のとある問題
[5] Wikipedia 「スプレー木」
[6] [2] の解説スライド
[7] yaketake08 さんの投稿「Splay Treeの可視化Webページを簡易的に作った」
[8] Daniel Sleator さんと Robert Tarjan さんの論文
[9] Wikipedia 「赤黒木」
[10] Wikipedia 「AVL木」
[11] 秋葉拓哉さんのスライド「プログラミングコンテストでのデータ構造２～平衡二分探索木編～」
[12] Daniel Sleator さんと Robert Tarjan さんの論文
[13] ながたかなさんの投稿「エッ！？平衡二分木の update, push (evel, propagate) のタイミングがわからないですって？フッフッフ……」

あとがき

そろそろ PCK で想定解が平衡二分探索木の問題が出そうで恐ろしく感じています。もし出たときも、平衡二分探索木のバグ取りは困難を極めるので、バグらせない決意を持って書き始めましょう。

Dynamic Sequence Range Affine Range Sum の TA 、あなたもいかがでしょうか。

動機の例

目標

導入

機能

原理

splay tree の特徴

均し（ 償却、 $\text{amortized}$ ）計算量

構造が柔軟

動的木への応用

実装・解説

基本構造(の基本）

実装の方針

実装例

基本構造（クエリ依存）

実装の方針

実装例

伝播・集約

実装の方針

実装の注意点

実装例

回転, splay

実装の方針

実装の注意点

図解・実装例

kth_element, insert, erase

実装の方針

実装の注意点

図解・実装例

between

実装の方針

実装の注意点

図解・実装例

reverse,apply, prod

実装の方針

実装の注意点

実装例

ゴール

注意点のまとめ

実装の注意点

実際にやってみた

補足

キーを用いて二分探索木として使いたい

定数倍高速化の例

link/cut tree をソラで書く！！？

実装の方針

実装の注意点

参考サイト一覧

あとがき

均し（償却、 $\text{amortized}$ ）計算量